Многогранник- это такое тело, поверхность которого состоит из конечной числа плоских многоугольников. Многогранник называется выпуклым, если он лежит по одну сторону от плоскости каждой из плоских многоугольников на его поверхности. Общая часть такой плоскости и поверхности выпуклого многоугольника называется гранью.
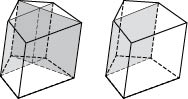
На рисунке ниже слева изображен неопуклий многогранник; на рисунке справа - выпуклый.

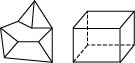
Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины граней - вершинами многогранника.

Призма

Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников (см. рисунок). Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины - боковыми ребрами призмы.

Обозначения: .
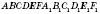
Боковая поверхность призмы состоит из параллелограммов. Каждый из них имеет две стороны, которые являются соответствующими сторонами основания, а две другие - смежными боковыми ребрами. Основания призмы равны и лежат в параллельных плоскостях. Боковые ребра призмы параллельны и равны. Высотой призмы называется расстояние между плоскостями ее оснований.
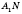
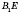
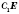
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы. (На рисунке - высота, и диагонали.)
Диагональные сечения - это сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани (см. рисунки).

Призма называется прямой, если ее боковые ребра перпендикулярны к основаниям. В противном случае призма называется наклонной.
Боковые грани прямой призмы - прямоугольники, высота прямой призмы равна боковому ребру, диагональные сечения являются прямоугольниками.
Боковой поверхностью призмы называется сумма площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Теорема 1. Боковая поверхность прямой призмы равна произведению периметра основания и высоты, то есть длины бокового ребра.
Перпендикулярным сечением призмы будем называть сечение плоскостью, перпендикулярной боковому ребру призмы (а это значит, что эта плоскость является перпендикулярной всех боковых ребер призмы).
Теорема 2. Боковая поверхность наклонной призмы равна произведению длины бокового ребра и периметра перпендикулярного сечения.
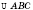
На рисунке - перпендикулярное сечение.
Sб = H ⋅ Pосн;
Sп = Sб + 2Sосн.
Sб = l ⋅ Pтэр;
Sп = Sб + 2Sосн.

Очевидно, что эта теорема верна и в случае прямой призмы, потому что тогда перпендикулярное сечение будет сечением плоскостью, параллельной плоскостям оснований призмы.
Обратите внимание: если некоторый многоугольник является перпендикулярным сечением призмы, то его внутренние углы являются линейными углами двугранных углов между соответствующими боковыми гранями.
В случае прямой призмы линейными углами двугранных углов между боковыми гранями являются непосредственно углы основания.
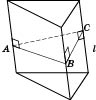
Пример
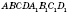
На рисунке - прямая призма.

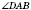
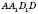
- линейный угол двугранного угла между гранями и .
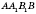
Призма называется правильной, если:
• в основе ее лежит правильный многоугольник;
• призма является прямой.

Параллелепипед

Собой параллелепипед называется призма, в основании которой лежит параллелограмм.
Все грани параллелепипеда - параллелограммы.
Грани параллелепипеда, не имеющие общих вершин, называются противоположными.
Теорема 1. Противоположные грани параллелепипеда являются параллельными и ровными.
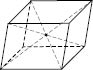
Параллелепипед остается собой параллелепипед во всех случаях, когда за его основу считаем любую его грань (см. рисунок).
Теорема 2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Из этого следует, что точка пересечения диагоналей параллелепипеда является его центром симметрии.
Обратите внимание: у прямого параллелепипеда имеются четыре диагонали, которые попарно равны друг другу.
На рисунке ; .
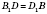
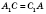
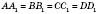
Это следует из свойств наклонных, так - равные перпендикуляры к плоскости основания ABCD.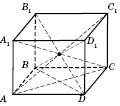

Если две диагонали прямого параллелепипеда выходящие из соседних вершин, то большая из них та, которая проектируется в большую диагональ основания, то есть такую диагональ параллелограмма, которая лежит против тупого угла. Следовательно, если на приведенном выше рисунке считать угол ABC тупой, получим , .
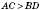
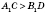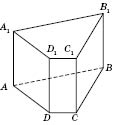
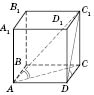
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным собой параллелепипед (см. рисунок).

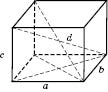
Все грани прямоугольного параллелепипеда - прямоугольники, которые можно разбить на три пары равных между собой. Произвольную грань прямоугольного параллелепипеда можно считать его основой. Учитывая, что при параллельном проектировании произвольный параллелограмм может изображаться произвольным параллелограммом, изображение прямоугольного параллелепипеда никак не отличается от изображения любого прямого параллелепипеда.
Длины непараллельных ребер называются линейными размерами (измерениями) прямоугольного параллелепипеда.
Теорема 3. В прямоугольном параллелепипеде все диагонали равны. Квадрат диагонали равен сумме квадратов трех его измерений.
Все двугранные углы прямоугольного параллелепипеда являются прямыми.
Прямоугольный параллелепипед имеет три пары равных между собой диагональных сечений. Каждый из этих сечений является прямоугольником (см. рисунки).

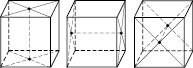
Каждая пара сечений пересекаются по прямой, проходящей через точки пересечения диагоналей противоположных граней. Отрезки между этими точками являются параллельными и равны одному из ребер прямоугольного параллелепипеда.
Прямоугольным треугольник, который образуется диагональю прямоугольного параллелепипеда, диагональю боковой грани и стороной основания (см. рисунок). Например, .

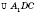
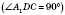
Прямоугольный параллелепипед имеет центр симметрии - это точка пересечения его диагоналей.
Он также имеет три плоскости симметрии, проходящие через центр симметрии параллельно граням.
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
Плоскость любого диагонального сечения куба является его плоскостью симметрии. Таким образом, куб имеет девять плоскостей симметрии.
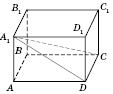
На рисунке рассмотрим взаимное расположение некоторых элементов прямого параллелепипеда:

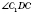
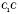
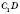
- угол между диагональю боковой грани и плоскостью основания ( - перпендикуляр, - наклонная, СD - проекция).
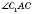
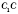
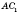
- угол между диагональю прямого параллелепипеда и плоскостью основания ( - перпендикуляр, - наклонная, АС - проекция).
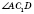
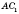
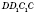
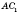
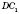
- угол наклона диагонали к боковой грани (AD - перпендикуляр, - наклонная, - проекция).
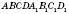
Пусть - прямой параллелепипед (см. рисунок), где ABCD - ромб. Проведем его сечение плоскостью, проходящей через диагональ основания BD и вершину .

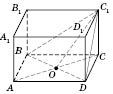
В сечении получим равнобедренный треугольник .
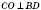
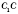
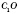
- линейный угол двугранного угла между плоскостями основания и сечения. по свойству диагоналей ромба, - перпендикуляр, - наклонная, СО - проекция. По теореме о трех перпендикуляры: .

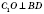
Пирамида

Пирамидой называется многогранник, который состоит из плоского многоугольника - основания пирамиды, точки, не лежащей в плоскости основания - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Высота пирамиды - перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида называетсяn-угольной, если ее основанием является n-угольник. Треугольная пирамида называется также тетраэдром. Боковая грань пирамиды - треугольник. Одной из его вершин является вершина пирамиды, а противоположной стороной - сторона основания пирамиды.
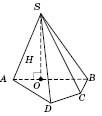
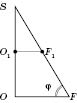
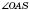
На рисунке SO - высота пирамиды. Тогда - угол между боковым ребром и плоскостью основания (SO - перпендикуляр, SА - наклонная, ОА - проекция).

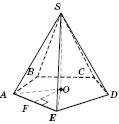
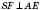
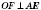
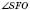
Из основания высоты пирамиды (точки В) проведем перпендикуляр на сторону основания (например, АЕ). Основание этого перпендикуляра (точка F) соединим с вершиной пирамиды (точка S). По теореме о трех перпендикуляры: . (SO - перпендикуляр, SP - наклонная, OF - проекция, по построению.) Следовательно, - линейный угол двугранного угла между плоскостью боковой грани ASEи плоскостью основания.
Для решения задач о пирамиде очень важно выяснять, где размещена основа ее высоты.
1. Если выполняется хотя бы одно из следующих условий:
• все боковые ребра пирамиды равны;
• все боковые ребра наклонены к плоскости основания под одним и тем же углом;
• все боковые ребра образуют одинаковые углы с высотой пирамиды;
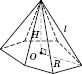
• все боковые ребра равноудалены от основания высоты, то основанием высоты пирамиды является центр окружности, описанной вокруг основания пирамиды.
Боковое ребро l, высота H и радиус R описанной вокруг основания окружности образуют прямоугольный треугольник:

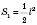
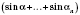
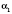
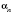
В этом случае боковую поверхность можно найти по формуле , где l - длина бокового ребра, , ... - плоские углы при вершине.
2. Если выполняется хотя бы одно из следующих условий:
• все боковые грани наклонены к плоскости основания под одним и тем же углом;
• все боковые грани имеют одинаковые высоты;
• высоты боковых граней образуют одинаковые углы с высотой пирамиды;
• боковые грани равноудалены от основания высоты, - то основание высоты лежит в центре круга, вписанного в основание пирамиды.
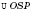
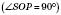
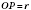
На рисунке - прямоугольный , - радиус вписанной окружности в ABCDEF;

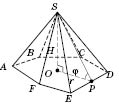
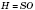
- высота пирамиды, SP - высота боковой грани;
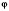
- линейный угол двугранного угла между боковой гранью и плоскостью основания;
О - центр вписанного в основание круга, то есть точка пересечения биссектрис ABCDEF.
В этом случае .
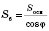
3. Если боковое ребро перпендикулярно к плоскости основания, то это ребро является высотой пирамиды (см. рисунки).

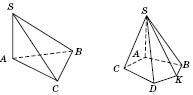
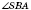
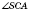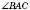
В этом случае и - углы наклона боковых ребер SВ и SС соответственно к плоскости основания. является линейным углом двугранного угла между боковыми гранями SAC и SBA.
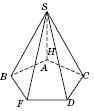
4. Если боковая грань перпендикулярна плоскости основания (см. рисунок), то высотой пирамиды будет высота этой грани (по теореме «Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна к прямой их пересечения, то она перпендикулярна второй плоскости»).
5. Если две боковые грани перпендикулярны к плоскости основания, то высотой пирамиды является их общее боковое ребро.

Расстояния от основания высоты пирамиды

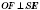
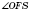
Расстояние от основания высоты пирамиды до бокового ребра - перпендикуляр, опущенный из точки О на это ребро (см. рисунок). Обратите внимание: , но на рисунке не должен быть прямым: углы при параллельном проектировании не сохраняются.
OF - расстояние от основания высоты до бокового ребра SE;
ON - расстояние от основания высоты до боковой грани ASB (о это расстояние подробнее смотри ниже).

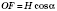
, где - угол между ребром SE и плоскостью основания.

Расстояние от основания высоты до боковой грани

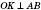
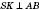
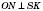
Пусть , тогда по теореме о трех перпендикуляры. Следовательно, AB перпендикулярна к плоскости SOK. Отсюда, если , то ON перпендикулярна к плоскости ASB.
.
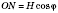
Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром многоугольника. Осью правильной пирамиды называется прямая, содержащая ее высоту. Боковые ребра правильной пирамиды равны, боковые грани - равные равнобедренные треугольники. Высота боковой грани, проведенная из вершины пирамиды, называется апофемою. Она является биссектрисой и медианой боковой грани, поскольку та является равнобедренным треугольником.
Теорема. Боковая поверхность правильной пирамиды равна произведению півпериметра основания на апофему.
; ,
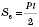
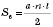
где Р - периметр основания, а - сторона основания, l - длина апофеми.
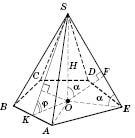
Правильная треугольная пирамида
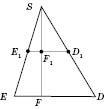
В основании правильной треугольной пирамиды лежит равносторонний треугольник, который изображается произвольным треугольником (см. рисунок).

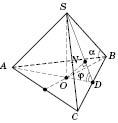
Центром является точка пересечения его биссектрис, которые одновременно являются высотами и медіанами. Медианы при параллельном проектировании изображаются медіанами. Поэтому строим две медианы основания. Точка их пересечения - основание высоты пирамиды. Изображаем высоту, а затем соединяем вершину пирамиды с вершинами основания. Получим боковые ребра.
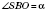
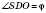
На рисунке: - угол наклона бокового ребра к плоскости основания (одинаковый для всех ребер); - угол наклона боковой грани к плоскости основания (одинаковый для всех граней).
Пусть .
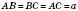
Тогда ; ; ;
; ; .
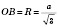
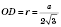
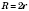
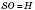
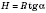
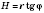
Следовательно, .
; .
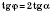
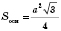
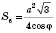
Плоскость осевого сечения ASD является плоскостью симметрии правильной треугольной пирамиды.
Эта плоскость перпендикулярна к плоскости основания и плоскости грани BSC.
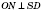
Интересно также отметить, что скрещивающиеся ребра пирамиды (SA и BC, SB и AC, SC и AB) являются перпендикулярными. Если , то ON является расстоянием от основания высоты не только к анафеме, но и к боковой грани BSC.
.
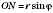
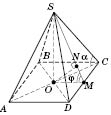
Правильная четырехугольная пирамида
В основании правильной четырехугольной пирамиды лежит квадрат, который изображается произвольным параллелограммом. Его центром является точка пересечения диагоналей. Эта точка - основание высоты пирамиды.
Пусть сторона квадрата а (см. рисунок).
Тогда ;
;
;
;
.

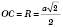
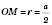
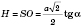
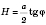
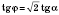
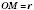
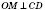
Обратите внимание: , , то есть .
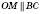
При параллельном проектировании сохраняется параллельность.
; .
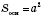
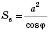
Расстояние от основания высоты до боковой грани:
; .

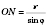
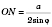
Правильная шестиугольная пирамида
В основе правильной шестиугольной пирамиды лежит правильный шестиугольник (см. рисунок). Его центром является точка пересечения диагоналей. Эта точка - основание высоты пирамиды.
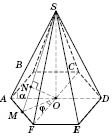
Тогда ;
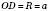
Пусть сторона правильного шестиугольника а.
;
;

.
; .

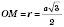
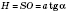
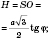
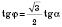
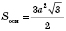
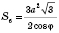
Усеченная пирамида
Срезанной пирамидой называется многогранник, который останется, если от пирамиды отделить плоскостью, параллельной основе, пирамиду с той же вершиной.
Теорема. Плоскость, которая параллельна основе пирамиды и пересекает ее, отсекает подобную пирамиду.
Обратите внимание: чтобы правильно изобразить срезанную пирамиду, надо начинать с изображения исходной полной пирамиды (см. рисунок).

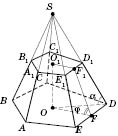
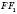
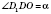
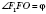
Основания усеченной пирамиды - подобные многоугольники. Боковые грани - трапеции. - высота усеченной пирамиды, - высота боковой грани, - угол наклона бокового ребра к плоскости основания (любой), - угол наклона боковой грани к плоскости нижнего основания.
Правильная усеченная пирамида - это усеченная пирамида, которую достали из правильной пирамиды.
Ее боковые ребра равны и наклонены к плоскости основания под одним и тем же углом. Ее боковые грани равны рівнобічній трапеции и наклонены к плоскости нижнего основания под одним и тем же углом. Высоты боковых граней пирамиды называются апофемами.
Боковая поверхность правильной усеченной пирамиды равна произведению половину суммы периметров оснований и апофеми.
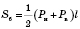
, где Pн и P - периметры соответствующих оснований, l - апофема.
На рисунках изображены фигуры, которые бывает очень полезным рассмотреть при решении задач на срезанную пирамиду.
;
.

;


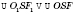
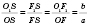
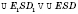
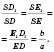
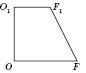
- прямоугольная трапеция.
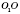
- высота усеченной пирамиды.
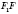- высота боковой грани.

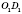
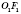
В случае, когда усеченная пирамида правильная, отрезки OD и являются радиусами описанной окружности, а OF и - радиусами вписанной окружности для нижней и верхней основы соответственно.

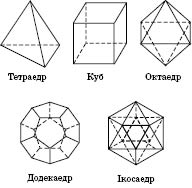
Правильные многогранники

Выпуклый многогранник называется правильным, если его грани являются правильными многогранниками с одним и тем же числом сторон и в каждой вершине многогранника совпадает одно и то же число ребер.
Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
1. У правильного тетраэдра грани - правильные треугольники; в каждой вершине совпадает по три ребра. Тетраэдр - треугольная пирамида, все ребра которой равны.
2. У куба все грани - квадраты; в каждой вершине совпадает по три ребра. Куб - прямоугольный параллелепипед с равными ребрами.
3. В октаэдра грани - правильные треугольники. В каждой его вершине совпадает по четыре ребра.
4. В додекаедра грани - правильные п'ятикутники. В каждой его вершине совпадает по три ребра.
5. В грани икосаэдра - правильные треугольники. В каждой его вершине совпадает по пять ребер.
На рисунках приведены примеры правильных многогранников с названиями.

Назад

Содержание

Вперед