Преобразования в пространстве

Понятие преобразования фигур в пространстве означают так же, как и на плоскости (см. раздел «Геометрия. 8 класс»).
Движением называется преобразование, при котором сохраняются расстояния между точками.
Свойства движения в пространстве:
Прямые переходят в прямые, півпрямі - в півпрямі, отрезки - в отрезки, углы между півпрямими сохраняются, плоскость переходит в плоскость.
Образцы движений в пространстве:
Симметрия относительно точки, симметрия относительно прямой; симметрия относительно плоскости (аналогичная симметрии относительно прямой).
Пример
Данная точка .
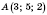
Найти точки, симметричные данной относительно координатных плоскостей.
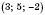
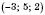
Ответ: точка, симметричная точке А относительно Оху, - это , относительно Oyz - это , относительно Oxz - это .
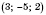
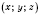
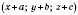
Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка переходит в точку , где числа a, b, c - одни и те же для всех точек .
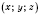
Параллельный перенос является движением.
В результате параллельного переноса точки смещаются вдоль параллельных прямых (или прямых, совпадающих) на одну и ту же расстояние.
1. В результате параллельного переноса каждая прямая переходит в параллельную ей прямую (или в себя).
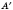
2. Каковы бы ни были точки А и в , существует единственный параллельный перенос, в результате которого точка А переходит в точку .
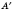
3. В результате параллельного переноса в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.