Перпендикуляр и наклонная
Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной к плоскости. Конец этого отрезка, лежащий в плоскости, называется
основанием перпендикуляра.
Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
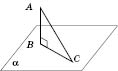
На рисунке
AB - перпендикуляр;
AC - наклонная;
BC - проекция.
 Расстоянием от прямой
Расстоянием от прямой до параллельной ей плоскости называется расстояние от любой точки этой прямой до плоскости.
Расстоянием между параллельными плоскостями называется расстояние от любой точки одной плоскости до другой плоскости.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости и не является перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется
основанием наклонной.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется
проекцией наклонной.
Свойства наклонных, проведенных из одной точки к одной плоскости
1. Наклонные, проведенные к плоскости из одной точки (рисунок ниже слева), равны тогда и только тогда, когда они имеют равные проекции.
2. Если из точки к плоскости проведены две наклонные, то больше та из них, которая имеет большую проекцию, и наоборот, большая наклонная имеет большую проекцию.
Обратите внимание, что эти свойства сохраняются для наклонных, проведенных к плоскости из разных точек, но имеют одинаковую длину перпендикуляра (рисунок справа).