Параллельность прямых и плоскости

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Прямые, которые не лежат в одной плоскости, называются скрещивающимися.
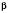
Обратите внимание: «не лежат в одной плоскости» и «лежат в разных плоскостях» - это разные утверждения. Например, параллельные прямые a и b лежат в разных плоскостях и (см. рисунок), но через них можно провести плоскость, содержащую a и b одновременно.

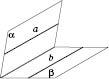
Для мимобіжних прямых (см. рисунок) не существует такой плоскости, в которой они лежали бы вместе.

Можно доказать, что все прямые, пересекающие две параллельные прямые, лежат в одной плоскости.
Теорема. Через точку, которая не лежит на данной прямой, можно провести прямую, параллельную данной, и только одну.