Аксиомы стереометрии

I. Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
II. Из трех точек на прямой одна и только одна лежит между двумя другими.
III. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
IV. Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
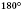
V. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
VI. На любой півпрямій от ее начальной точки можно отложить отрезок данной длины, и только один.
VII. От півпрямої на плоскости, содержащей ее, можно отложить в заданную півплощину угол с данной градусной мере, меньше , и только один.
VIII. Каков бы ни был треугольник, существует треугольник, равный ему, в данной плоскости в заданном размещены относительно данной півпрямої в этой плоскости.
IX. На плоскости через данную точку, не лежащую на данной прямой, можно провести более чем одну прямую, параллельную данной.
В этих аксиом прилагаются три аксиомы группы С.
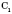
. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и к тому же только одну.
Теорема 1. Через прямую и точку, не лежащую на ней, можно провести плоскость, и к тому же только одну.
Теорема 2. Через прямую можно провести две различные плоскости (см. рисунок).

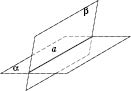
Теорема 3. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Следовательно, возможны три варианта взаимного расположения прямой и плоскости в пространстве.
1. Прямая лежит в плоскости (рисунок слева).
2. Прямая пересекает плоскость в данной точке (рисунок справа).

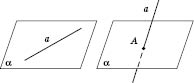
3. Прямая не пересекает плоскость (см. рисунок). В данном случае прямая а называется параллельной плоскости.

Теорема 4. Через три точки, не лежащие на одной прямой, можно провести плоскость, и к тому же только одну.
Для решения задач могут быть полезными такие утверждения.
1. Если две различные прямые пересекаются в некоторой точке (рисунок ниже слева), то все прямые, которые пересекают обе данные прямые и не проходящие через эту точку, лежат в одной плоскости.
2. Все прямые, которые пересекают данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости (рисунок справа).