Решение треугольников

Решение треугольников состоит в нахождении неизвестных сторон и углов треугольника по известным его сторонами и углами.
Результаты в таких задачах приближенные, потому что для большинства значений углов приближенными есть их значение синуса и косинуса.
Задача 1. Решить треугольник по стороной и двумя прилежащими углами.
На рисунке в треугольнике дано: a; ; .
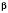
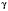
Найти: ; b; c.

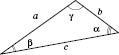Решение
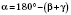
1) (по теореме о сумме углов треугольника).
2) По теореме синусов:
.
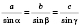
Итак, , ,, .
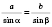
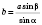
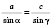
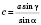
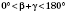
Задача имеет решение всегда, когда , причем это решение будет единственным.
Задача 2. Решить треугольник с двумя сторонами и углом между ними.
Дано: a; b; .
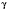
Найти: c; ; .
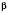
Решение
1) По теореме косинусов:
;
.
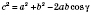
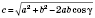
2) По теореме косинусов: .
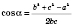
По таблицам или с помощью калькулятора находим приближенное значение .
3) По теореме о сумме углов треугольника: .
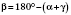
Задача всегда имеет решение, причем решение будет единственным.
Обратите внимание: при решении задачи 2 для нахождения неизвестных углов можно пользоваться теоремой синусов. Но тогда целесообразно начинать с того неизвестного угла, который будет меньшим, то есть лежит против меньшей стороны. Этот угол обязательно будет острым, то есть по значению его синуса можно будет определить единственное значение угла.
Задача 3. Решить треугольник с двумя сторонами и углом, противоположным одной из этих сторон.
Дано: a; b; .
Найти: c; ; .
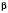
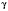
Решение
1) По теореме синусов:
; .
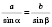
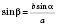
По таблицам или с помощью калькулятора находим приближенное значение .
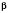
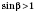
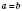
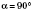
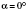
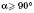
Обратите внимание: на этом этапе можно получить . Тогда задача не имеет решений. Если по условию , или , или , задача тоже не имеет решения.
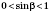
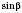
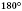
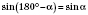
Если мы получим , задача будет иметь два решения, потому что одно и то же значение будет в двух углов - тупого и острого, которые в сумме дают . (За тождественностью .) Дальнейшее решение тогда проводят отдельно для каждого значения .
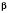
2) По теореме о сумме углов треугольника:
.
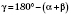
3) По теореме синусов:
; .
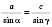
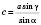
Задача 4. Решить треугольник по трем сторонам.
Дано: a; b; c. Найти: , , .
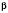
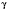
Решение
1) По теореме косинусов:
; .
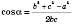
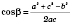
Находим приближенные значения и .
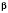
2) По теореме о сумме углов треугольника: .
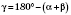
Задача не будет иметь решений, если наибольшее из данных сторон не меньше суммы двух других. В других случаях задача имеет одно решение.