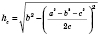Теорема косинусов

Теорема (косинусов). Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон и косинуса угла между ними.
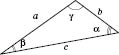
В треугольнике, изображенном на рисунке, по теореме косинусов: .


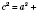
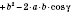
Теорему косинусов удобно применить для решения таких задач.
1. Найти сторону треугольника, если известны две другие стороны и угол между ними.
2. Найти косинус углов треугольника, а следовательно и сами углы, если известны три стороны треугольника, по формуле .
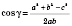
Теорема косинусов дает возможность сформулировать важные выводы.
1. Известно, что острый угол имеет положительный косинус, а тупой - отрицательный. Следовательно, квадрат стороны, лежащей против тупого угла, больше суммы двух других сторон, а квадрат стороны, лежащей против острого угла, меньше, чем сумма двух других сторон.
2. Если известны три стороны треугольника, то можно сделать вывод о его вид (остроугольный, тупоугольный, прямоугольный). Для этого надо сравнить квадрат наибольшей стороны с суммами квадратов двух других сторон. Если квадрат наибольшей стороны треугольника больше, чем сумма квадратов двух других сторон, то треугольник тупоугольный, если величины уровне - прямоугольный, если первая величина меньше - остроугольный.
3. В случае, когда прямоугольный треугольник, теорема косинусов для стороны, лежащей против прямого угла, превращается в теорему Пифагора.
4. Из теоремы косинусов следует, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
На рисунке .

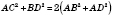
5. Формула длины медианы треугольника: в треугольнике, изображенном на рисунке, .

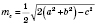
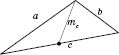
6. Формула длины биссектрисы треугольника: в треугольнике, изображенном на рисунке, .

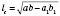
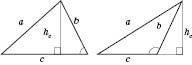
7. Формула высоты треугольника: на рисунке слева изображена высота в гострокутному треугольнике, на рисунке справа - в тупокутному.