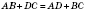Пропорциональность отрезков хорд и секущих окружности
Теорема 1. Если хорды
AB и
CD окружности пересекаются в точке
S, то
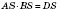
(рисунок 1).
Теорема 2. Если из точки
P к окружности проведены две секущие, пересекающие окружность соответственно в точках
A,
B,
C,
D, то
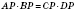
(рисунок 2).
То есть произведение секущей, проведенной к окружности из данной точки на ее внешнюю часть, является число неизменно.
Теорема 3. Если из точки
P к окружности проведены касательная, проходящая через точку касания
A, и секущая, которая пересекает окружность в точках
B и
C, то
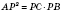
(рисунок 3).
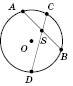
Рис. 1
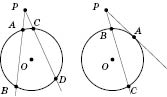
Рис. 2 Рис. 3
То есть для секущей и касательной, проведенных к окружности из одной точки, квадрат касательной равен произведению секущей на ее внешнюю часть.
Теорема 4. Хорды, соединяющие концы параллельных хорд, уровне.
Вписанные и описанные четырехугольники
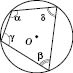
Теорема 1. Вокруг четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна
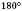
.
На рисунке
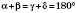
.
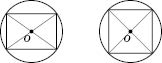
Из этого следует, что круг можно описать вокруг прямоугольника (рисунок ниже слева), в частности квадрата (рисунок справа), его центром будет точка пересечения его диагоналей. Радиус - половина диагонали.
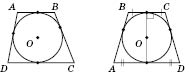
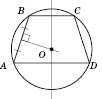
Круг можно описать вокруг трапеции тогда и только тогда, когда она является рівнобічною (см. рисунок). Центром окружности является точка пересечения средних перпендикуляров к сторонам. Вокруг параллелограмма и трапеции общего вида описать круг нельзя. (В частности, вокруг ромба можно описать окружность.)
Теорема 2. Четырехугольник тогда и только тогда можно описать вокруг окружности, если суммы его противоположных сторон равны друг другу.
На рисунке
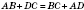 .
.
Итак, круг можно вписать в ромб (в частности в квадрат), но нельзя в прямоугольник или параллелограмм общего вида.
Центр круга, вписанного в ромб, является точкой пересечения диагоналей (рисунок ниже слева). Радиус окружности равен половине высоты ромба, а в квадрате - половине стороны (рисунок справа).
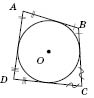
Обратите внимание: радиус вписанного в ромб круга (
ON) - это высота прямоугольного треугольника
BOC, которая проведена из вершины прямого угла и имеет все свойства высоты прямоугольного треугольника, проведенная из вершины прямого угла.
Теорема 3. Трапецию тогда и только тогда можно описать вокруг окружности, когда сумма ее оснований равна сумме боковых сторон (рисунок ниже слева). Центр этой окружности - точка пересечения биссектрис углов трапеции. Радиус равен половине высоты трапеции. В случае рівнобічної трапеции центр вписанной окружности лежит на середине высоты трапеции, которая проходит через середины оснований (рисунок справа). Боковая сторона трапеции в этом случае равна ее средней линии.