Симметрия относительно точки

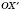
Пусть O - фиксированная точка, X - произвольная точка плоскости. Отложим на продолжении отрезка OX точки O отрезок , равный OX.
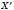
Точка называется симметричной точке X относительно точки O(см. рисунок).

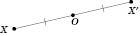
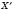
Очевидно, что точка, симметричная , является точка X.
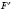
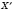
Преобразование фигуры F в фигуру , при котором каждая ее точка X фигуры F переходит в точку , симметричную относительно точки O, называется преобразованием симметрии относительно точкиO.
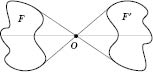
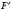
Фигуры F и называются симметричными относительно точкиO (см. рисунок).

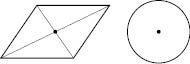
Если преобразование симметрии относительно точки O переводит фигуру F в себя, то фигура F называется центрально-симметричной, а точка O - ее центром симметрии. Например, точка пересечения диагоналей параллелограмма является его центром симметрии (рисунок ниже слева). Центр круга является его центром симметрии (рисунок справа).

Теорема. Преобразование симметрии относительно точки является движением.