Неравенство треугольника
Теорема. Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.
Отсюда следует, что в любом треугольнике каждая сторона меньше суммы двух других сторон, но больше модуль разности двух других сторон.
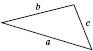
Если
a,
b и
c - стороны треугольника (см. рисунок), то
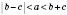
;
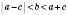
;
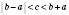
.