Геометрия
Треугольники
Перпендикуляр и наклонная
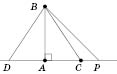
Пусть BA - перпендикуляр, опущенный из точки B на прямую a, а С - любая точка прямой a, отличная от A (см. рисунок). Отрезок BC называется наклонной, проведенной из точки B к прямой a. Точка С называется основанием наклонной. Отрезок АС называется проекцией наклонной. 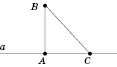 Свойства наклонных
Теорема. Когда из данной точки к прямой проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра; равные наклонные имеют равные проекции, а из двух наклонных больше та, у которой проекция больше. На рисунке BD, BC, BP - наклонные, AB - перпендикуляр, 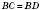 ; 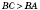 ; 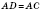 . .
|
|