Средняя линия треугольника

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Теорема 1. Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.
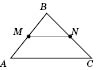
На рисунке справа:
;.

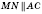
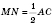
В треугольнике можно провести три средние линии. Они образуют треугольник с такими же углами, как настоящее, и вдвое меньшими сторонами.
На рисунке ниже ABC - треугольник; MN, NK, MK - его средние линии.
Четырехугольники AMNK, BNKM, MNCK - параллелограммы.

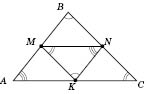
Теорема 2. Средняя линия треугольника делит пополам высоту, бісектрису, медиана треугольника, проведенные к параллельной ей стороны:

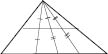
Опираясь на свойство средней линии, легко доказать, что:
1) середины сторон четырехугольника являются вершинами параллелограмма (рисунок 1);
2) середины сторон прямоугольника являются вершинами ромба (рисунок 2);
3) середины сторон ромба являются вершинами прямоугольника (рисунок 3);

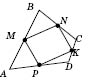
Рис. 1


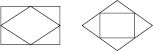
Рис. 2 Рис. 3
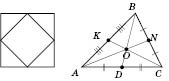
4) середины сторон квадрата являются вершинами квадрата (рисунок ниже слева);
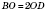
5) медианы произвольного треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины ( и т. д.) (рисунок справа).