Квадрат
Квадрат - это прямоугольник, у которого все стороны равны.
Свойства квадрата
Поскольку квадрат является параллелограммом, прямоугольником и ромбом в то же время, имеем:
1) у квадрата все стороны равны;
2) у квадрата все углы равны;
3) диагонали квадрата равны, пересекаются под прямым углом, делятся в точке пересечения пополам, есть бісектрисами его углов;
4) диагонали квадрата делят его на четыре равные равнобедренные прямоугольные треугольники.
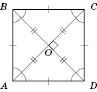
На рисунке
ABCD - квадрат.
AB = =
BC =
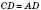
;
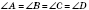
;
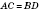
;
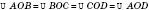
.
Признаки квадрата
Теорема 1. Если у четырехугольника все стороны и все углы равны, то он является квадратом.
Теорема 2. Если диагонали прямоугольника пересекаются под прямым углом, то он является квадратом.
Теорема 3. Если диагонали ромба равны, то он является квадратом.