Круг
Кругом называется фигура, состоящая из всех точек плоскости, равноудаленных от данной точки. Эта точка называется
центром круга.
Расстояние от точек окружности к ее центра называется
радиусом окружности. Радиусом называется любой отрезок, соединяющий точку окружности с его центром.
Отрезок, соединяющий две точки окружности, называется
хордой. Хорда, проходящая через центр окружности, называется
диаметром.
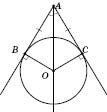
На рисунке изображена окружность с центром в точке
O.
OA - радиус круга,
MN - диаметр,
ВС - хорда.
Теорема 1. Диаметр, перпендикулярный к хорде, делит ее пополам.
Теорема 2. Диаметр, проходящий через середину хорды, перпендикулярен к ней.
Серединным перпендикуляром к отрезка называется прямая, проходящая через середину отрезка перпендикулярно к нему.
Окружность называется
описанной вокруг треугольника, если она проходит через все его вершины.
Теорема 3. Вокруг любого треугольника можно описать окружность. Его центр - точка пересечения серединных перпендикуляров к сторонам треугольника.
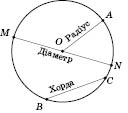
Обратите внимание: в гострокутному треугольнике центр описанной окружности лежит в середине треугольника (рисунок ниже слева). В прямоугольном треугольнике центр описанной окружности - середина гипотенузы (рисунок посередине). Центр круга, описанного вокруг тупокутного треугольника лежит вне треугольника (рисунок справа).
Касательная к окружности
Прямая, проходящая через точку окружности перпендикулярно к радиусу, проведенному в эту точку, называется
касательной. Данная точка круга называется
точкой касания.
Теорема 1. Касательная к окружности имеет с ним единственную общую точку - точку касания.
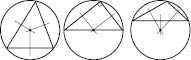
На рисунке
a - касательная.
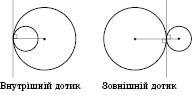
Если две окружности, имеющие общую точку, имеют в ней общую касательную, говорят, что эти
круги соприкасаются. Касание окружностей называют
внутренним, если центры окружностей лежат по одну сторону от их общей касательной (рисунок ниже слева), и
внешним, если центры окружностей лежат по разные стороны от общей касательной (рисунок справа).
Круг называется
вписанным в треугольник, если она касается всех его сторон.
Теорема 2. В любой треугольник можно вписать окружность. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Теорема 3. С любой точки вне круга можно провести к окружности две касательные. Отрезки этих касательных от данной точки до точек касания равны. Луч, выходящий из данной точки и проходит через центр окружности, является биссектрисой угла между касательными.
На рисунке ниже
AB и
AC - касательные. Теорема утверждает, что
AB =
AC;
AO - биссектриса
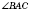
.