Урок № 98

Тема. Решение линейных уравнений с одной переменной

Цель: сформировать представление о содержании понятия «линейное уравнение с одной переменной» и способы его решения; отработать навыки решения уравнений, сводящихся к линейным.

Тип урока: применение знаний, умений и навыков.

Ход урока

I. Организационный момент

II. Проверка домашнего задания

1. Проводим выборочно, взяв в нескольких учеников тетради для проверки.

2. Для диагностики уровня усвоения свойств (равносильности) уравнений проводим небольшую самостоятельную работу, которую проверяем сразу по окончании.

Самостоятельная работа

Решите уравнение:

Вариант 1 [2]

а) 7х + 3 = 30 - 2х; б) 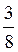х + 15 = 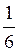х + 10; в) 0,3(х - 2) = 0,2 х + 2

[а) 8х - 8 = 20 - 6х; б) 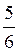х + 16 = 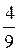х + 9; в) 2,7 + 3y = 9(y - 2,1)]

III. Воспроизведение знаний

@ Во время проверки правильности выполнения самостоятельной работы учащиеся повторяют и воспроизводят свои знания относительно:

а) свойств уравнений;

б) алгоритма решения уравнений;

в) правил выполнения арифметических действий с рациональными числами
свойствами этих действий.

IV. Формирование знаний

@ По сути единственным новым понятием урока является понятие линейного уравнения с одной переменной; на интуитивном уровне ученики это понятие уже усвоили (вспомним алгоритм решения уравнений, рассмотренный на предыдущем уроке). Поэтому просто возвращаемся к решенных примеров и обращаем внимание на то, что все решены до сих пор уравнения приводили к виду ах = b, где а и b - некоторые числа. Такие уравнения мы будем называть линейными уравнениями с одной переменной.

Заметим, что иногда линейными уравнениями с одной переменной называют и такие уравнения, которые можно привести к виду ах = b, выполнив упрощение выражений в правой и левой частях уравнения и сделав перенос слагаемых из одной части уравнения в другую.

Также важно подчеркнуть, что при а ≠ 0 линейное уравнение обязательно имеет рациональный корень, то есть корнем является число, которое может быть записано в виде 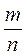. Поэтому во время решения уравнений вида ах = b, где а ≠ 0, лучше х записать как 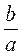, а потом уже превращать это выражение (а не делить b на а «уголком», потому что часто будем иметь бесконечный периодический дробь).

V. Закрепление знаний. Отработка навыков

Устные упражнения

1. Какие из уравнений являются линейными?

а) 3х = 6; б) -3х = 5; в) -3х = 0; г) -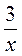 = 0; д) - 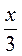= 0.

2. Решите линейное уравнение:

а) 3х = 6; б) -3х = 6; в) -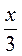= 6; г) -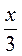= 0; д) * + 0х = 6; е) * 0х = 0.

@ Поскольку схема решения линейного уравнения с одной переменной при любых значениях а и b дается в 7 классе, на этом этапе мы рассматриваем в основном случаи, когда а ≠ 0, а остальные возможные случаи только на интуитивном уровне (для сильных, подготовленных классов).

Письменные упражнения

1. Решите уравнение:

а) 0,5 х + 3 = 0,2 х;

б) -0,4 а - 14 = 0,3a;

в) 2х - 6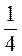 = 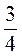x + 7;

г) 6,9 - 9a = -5a - 33,1;

д) 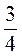k - 12,5 = 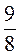k - ;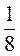

есть) 4,7 - 8z = 4,9 - 10z;

ж) 7,3 а = 1,6 а;

с) -19t = 11t;

к) 3(4х - 8) = 3х - 6;

л) -3,2x + 4,8 = -2 · (1,2х + 2,4);

г) -5 · (0,8z - 1,2) = z + 1,2;

н) 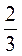·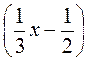= 4х + 2.

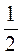2. Найдите значение выражения .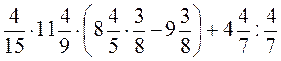

VI. Итог урока

Какое уравнение называют линейным с одной переменной? Приведите пример линейного уравнения с одной переменной, корень которого равен:

а) 1; б) -2; в) 0; г) любому числу.

VII. Домашнее задание

1. Решите уравнение:

а) 4(х - 6) = х - 9;

б) 6 - 3(х + 1) = 7 - х;

в) (8х + 3) - (10х + 6) = 9;

г) 2,8 - х = 8(х + 2,8);

д) 0,3(6 - 3y) = 4,5 - 0,8(y - 9);

есть) ;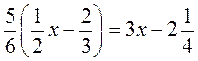

ж) 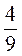x + 14 = 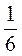x + 9.

2. Найдите значение выражения 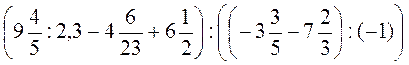.