|
2. Сведите подобные слагаемые: а) 3m + 2m + 4m; б) 3m - 2m + 4m; в) 3m + 2m - 4m; г) 3m - 2m - 4m; д) -3m - 2m - 4m. 3. Среди уравнений найдите такие, которые имеют одинаковые корни (не решая уравнений): а) 3х - 4 = х + 5; б) 3х - х = -4 + 5; в) 3х - х = 5 + 4; г) 3 = 9; д) 2х = 9; е) 2х = 1; ж) 2х = -1.
III. Актуализация опорных знаний Устные упражнения 1. Решите уравнения и сравните их корни: 3(х + 2) = 12; х + 2 = 12 : 3. 2. На какое число можно умножить данные группы чисел, чтобы достать в произведениях только натуральные числа? а)
IV. Мотивация учебной деятельности @ На этом этапе урока нужно дать понять учащимся, что свойства уравнений, которые они рассмотрели на предыдущем уроке и которые рассмотрят сегодня, является инструментом, который помогает упрощать решения уравнений.
V. Формирование знаний @ Свойство уравнения, которую автор также предлагает дать ученикам, является основой для понимания алгоритмов решения дробных уравнений (8 кл.) и многих линейных уравнений (7 кл.), и использование этого свойства для решения уравнений, содержащих дроби (рациональные или обычные), по опыту автора, вызывает определенные трудности в семи-и восьмиклассников. Поэтому считаем целесообразным начать работу по выработке умений применения этого свойства равносильности уравнений уже в 6 классе. 1. Решите уравнение 4(х + 5) = 12. (1) Решения. По правилу нахождения неизвестного множителя, х + 5 = 12.4, т.е. х + 5 = 3. Отсюда х = 3 - 5, х = -2 2. Решите уравнение(4(х + 5)) : 4 = 12 : 4. (2) Решения. По свойству деления, имеем: 4(х + 5) : 4 = х + 5, 12 : 4 = 3, поэтому х + 5 - 3, х = 3 - 5, х = 2. Сравнив (1) и (2) и их решения, приходим к выводу: Корни уравнения не изменяются, если его обе части умножить или разделить на одно и то же число, не равное 0. Пример. Решите уравнение Решения. Умножим обе части уравнения на 3:
Далее решаем уравнение, перенеся неизвестные слагаемые в одну часть, а известные оставляя в другой. 3х - х = 36; 2х = 36; х = 18. Проверка: Следовательно, если уравнение содержит дробные коэффициенты, можно избавиться от этих дробей, умножив правую и левую части уравнения на знаменатель (общий) этих дробных коэффициентов.
VI. Закрепления знаний. Выработка умений Устные упражнения 1. На какое число можно разделить правую и левую части уравнения, чтобы получить уравнение с цілочисленими коэффициентами? а) 2. Выполните умножение: Письменные упражнения 1. Выполнив умножение обеих частей уравнения на одно и то же число, избавьтесь от дробных чисел и решите уравнение: а) б) -2 в) г) д) есть) ж) 0,2 х + 2,3 = 0,7 х - 3,2. 2. Поделив обе части уравнения на одно и то же число, не равное 0, решите уравнение: а) -40 · (-7х + 5) = -1600; б) (-20х - 50) · 2 = 100; в) 2,1 · (4 - 6в) = - 42; г) -3 · (2 - 15х) = -6. Упражнения на повторение 3. При каком значении а значение выражения-3а + 11 и 7а - 1 уровне? 4. Логическая упражнение дополнительно. Найдите пропущенное число:
VII. Итоги урока 1. Обе части уравнения умножили на -3; 2. Обе части уравнения разделили на -0,3; 2. Изменились ли корни уравнение?
VIII. Домашнее задание 1. Решите уравнение: а) 2 - б) х - 2 в) 1 г) д) 2. Решите уравнение (разделив правую и левую часть уравнения и выполните проверку. а) -20 · (х - 13) = -220; б) (30 - 7х) · 8 = 352; в) (2,8 - 0,1 х) · 3,7 = 7,4; г) (3х - 1,2) · 7 = 10,5. 3. Раскройте скобки и сведите подобные слагаемые: а)3(в - 5) - 2(в - 4); б) -5(5 - х) - 4х; в) г) 5,4(3у - 2) - 7,2(2у - 3); д) есть)
|
|
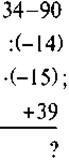
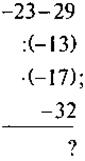
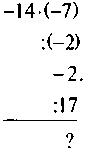
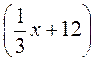 ·3 = х · 3; х + 36 = 3х или 3х = х + 36.
·3 = х · 3; х + 36 = 3х или 3х = х + 36.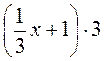 ;
; 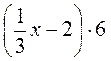 .
.
