Урок № 95

Тема. Уравнения. Основное свойство уравнения

Цель: повторить и обобщить знания учащихся о содержании понятия «уравнение» и связанных с ним понятий и способы решения уравнений, известные учащимся из начальной школы и 5 класса; сформировать представление об основных видах равносильных преобразований линейных уравнений с одной переменной (на интуитивном уровне); начать работу по выработке умений выполнять основные равносильные преобразования уравнений для их решения.

Тип урока: усвоение новых знаний.

Ход урока

I. Организационный момент

II. Актуализация опорных знаний

Устные упражнения

1. Вычислите:

2. Используя правила нахождения неизвестных компонентов арифметических действий, решите уравнение (найдите корень уравнения):
а) х - 2,2 = -0,8;

б) х + 2,2 = -0,8;

в) х · (-2,2) = -0,8;

г) х : (-2,2) = -0,8;

д) -2,2 : х = -0,8;

е) -2,2 - х = -0,8;

ж) (х - 3)(х - 2) = 0.

3. Упростите выражение:

a) 5a - 7a + 8b - 2b;

б) 3х - 4у - х - у;

в) х - (2х - 1);

г) -(х + 1) + (х - 1);

д) -2(а - 3);

ж) -0,2(-2а + 0,3).

III. Мотивация учебной деятельности

@ Задача. На одной чаше весов лежат два одинаковых бруска мыла, на другой один такой брусок и еще гирька массой 100 г. Сколько весит один брусок мыла?

Решения. Понятно, что один брусок весит 100 г. Но если записать уравнение, соответствующее условию задачи, приняв массу бруска мыла по х (г), будем иметь: 2х = х + 100 - видим, что неизвестное находится в разных частях уравнения. Такие уравнения мы пока решать не умеем. Следовательно, надо узнать про определенное свойство, которое поможет нам решить уравнения, имеющие неизвестные в разных частях уравнения (учитель сообщает тему урока).

IV. Повторение и систематизация знаний

@ Прежде чем разобрать с учащимися основные виды равносильных преобразований уравнений, желательно повторить и систематизировать знания о уравнения, которые учащиеся должны иметь на это время, а именно:

· содержание понятия «уравнение» (равенство, в котором есть неизвестное число);

· корень уравнения (значение переменной, которое превращает уравнение в верное равенство);

· что значит «решить уравнение» (найти все корни или доказать, что их нет);

· какие правила мы использовали до этого момента во время решения
уравнений (зависимости между компонентами арифметических действий и свойство нуля при умножении).

V. Формирование знаний

@ После проведенного повторения и систематизации знаний учащихся мы на интуитивном уровне формируем представление о основные виды равносильных преобразований уравнений. Формировать такие представления можно с помощью использования наглядно-предметных средств, в частности представление о терезы, что в равновесии (если на обе чаши весов, находящихся в равновесии, положить гирьки одинаковой массы или с обеих чаш таких весов убрать гирьки одинаковой массы, то весы останутся в равновесии).

Таким образом формируем представление о первой свойство уравнений:

Корни уравнения не изменятся, если какое-либо слагаемое (слагаемые) перенести из одной части уравнения в другую, изменив при этом его знак на противоположный).

И если сам этот вывод для большинства учеников понятен, то его применение требует кропотливой работы.

VI. Закрепления знаний. Выработка умений

Устные упражнения

1. Правильно ли выполнен перенос слагаемых из одной части в другую в уравнении: 2х - 3 = х - 7?

а) 2х - 3 - х - 7 = 0;

б) 2х - х = -7 - 3;

в) -2х + х = -7 + 3;

г) 2х - х = 7 + 3.

2. Объясните каждый шаг решения уравнения:

7х - 14 = 5х; 7х - 5х = 14; 2х = 14; х = 14 : 2; х = 7.

Письменные упражнения

@ Перед развязыванием письменных упражнений следует еще раз объяснить, что переносить из одной части уравнения в другую можно только слагаемые; переносят слагаемые так, чтобы в одной части уравнения были известны числа, а в другой - неизвестные.

1. Перенесите из левой части уравнения в правую слагаемое, которое не содержит неизвестного: а) -5х + 1,2 = 2х + 11; б) 4х - 9 = -х - 5,2.

2. Перенесите в левую часть уравнения все слагаемые, содержащие неизвестное, а в правую, не содержащие неизвестного: а) 17х - 5 = 8х + 5,6; б) -11у + 7 = -3у - 10.

3. Решите уравнение:

а) 7х - 5 = 6х + 1;

б) 4х - 3 = 2х + 5;

в) 9 - 8у = -6у + 1;

г) 6m + 3 = 7m + 8;

д) -9m - 2 = 9m - 2;

е) -9а + 6 = -10а + 15;

ж) 4у + 7 = -5 + 4у;

с) 0,7 х + 1,6 = -0,1 х;

к) -4,5 х - 3 = 2,7 х + 15;

л) 39 - 7у + 17 = 3y + 16;

г) 15 - 6х = 2х - 5х - 3.

@ (Прежде чем переносить слагаемые, надо упростить выражения в правой и левой частях отдельно (свести подобные слагаемые, если они есть).

Логическая задача

4. Найдите пропущенное число:

VI. Итоги урока

Сформулируйте правило переноса слагаемых из одной части уравнения в другую. Или имеют одинаковые корни уравнения 2х - 3 = х + 5 и 2х - х = 5 - 3? Почему?

VII. Домашнее задание

1. Решите уравнение:

а) 5х - 5 = 2х - 7;

б) х - 9 = 3х - 6;

в) 4,5 в + 1 = -5 + 5у;

г) 11х - 1,8 = 7х + 1,4;

д) 5,6 х - 1 = -1 + 6х;

e) 5,7m - 13,75 = 8,2m.

2. Упростите выражение:

а) 5m - (3m + 5) + (2m - 4);

б) -5(х + 3) + 4(х - 2) - 6(2х + 1);

в) 0,2(6х - 5) - 4(0,2 х - 2);

г) 0,4(1,5y + 3) -2,5(3 - 0,6y);

д) ;

е) .

3. Задача. К некоторому числу прибавили 62, полученную сумму умножили на 3 и получили 32. Найдите неизвестное число.
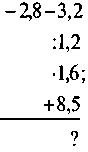
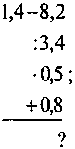
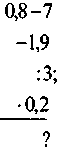
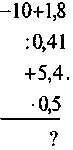
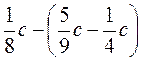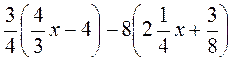