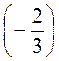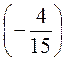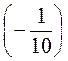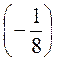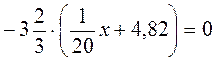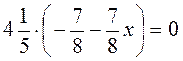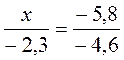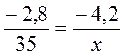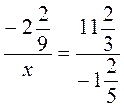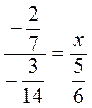Урок № 90
Тема. Деление рациональных чисел
Цель: закрепить знания и отработать навыки использования правила деления рациональных чисел отдельно и вместе с другими правилами арифметических действий над рациональными числами.
Тип урока: применение знаний, умений и навыков.
Ход урока
И. Проверка домашнего задания
@ Поскольку единственный новый момент, который был разобран на предыдущем уроке - это определение знака доли двух рациональных чисел, то проверяем этот момент. Именно на доске учитель или один ученик записывает зашифрованные ответы (только знаки долей)). Например:
1. Найдите долю:
а) 3,6 : (-4); б) 2,5 : (-7,5); в) - 8,64 : 1,2; г) - 56,68 :(-0,01); д) -2 : 0,05; е) -3 : 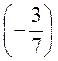 ; ж)
; ж) 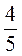 :
: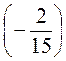 ;)
;) 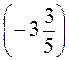 :
: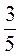 ; ы)
; ы) 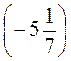 :
: .
.
а) -; б) +; в) -; г) +; д) -; е) +; в) -;) -; в) +; и) +.
Таким образом, экономим время на проверке домашнего задания.
2. В начале урока можно дать математический диктант.
Математический диктант
Вариант 1 [2]
1. Выполните деление на 1,8 -2 [-2,4 на -4].
2. Можно вычислить долю 0 и (-5) [-8 и 0]?
3. Можно ли вычислить значение выражения -6 поделить на 0 [0 поділіти на -3]?
4. Решите уравнение: -0,25 х = 5[в : (-0,5) = -7]; с : (-2,3) = -2 [-0,34a = 0,68].
II. Актуализация опорных знаний
Во время проверки правильности выполнения математического диктанта повторяют правила и некоторые свойства деления. Чтобы полностью подготовить учащихся к решению упражнений, запланированных на этот урок, решаем устные упражнения.
Устные упражнения
1. Поставьте вместо * знаки действий, чтобы выполнялся порядок действий, указанный римскими цифрами. Можно пользоваться скобками.
а) 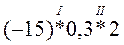 ; б)
; б) 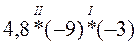 ; в)
; в) 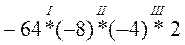 .
.
2. Упростите выражение: а) 3(2х - 11); б) -2(5 - 2х); в) -5(x + 3) + 3.
III. Отработка навыков
@ Если правила деления рациональных чисел усвоены учениками хорошо, на этом уроке решаем упражнения более высокого уровня сложности, а именно та, предусматривающих применение других правил арифметических действий с рациональными числами и их свойства.
Устные упражнения
1. Вычислите долю:
-12 : 3
-24 : (-6)
100 : 125
-6,25 : 2,5 |
0 : (-8.7)
-1 : (-1)
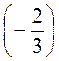 :1 :1
-0,16 : (-8) |
-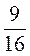 : : 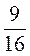
-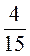 : : 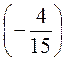
10 : 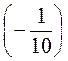
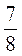 : : 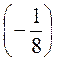
|
2. Игровой момент
На доске записаны следующие примеры:
-2,5 · 3 = ...; 5,3 · (-2) = ...; -5,5 · (-4) = ...; -7,1 · 10 = ...; -15,3 : (-3) = ...; 20,5 : (25) = ...; -27,9 : 9 = ...; -15,2 : 10 = ....
Учитель называет число, а ученики находят, результатом действия которой является это число. (Например, учитель говорит: «-3,1». Ученик отвечает: «-27,9 : 9 = -3,1»). Повторяем несколько раз.
3. Игровой момент
Учитель. Я задумал 2 числа. Поставьте только 1 вопрос и, выслушав ответ, скажите, числа имеют одинаковые знаки?
Письменные упражнения
1. Вычислите:
а) (-28) : (-4) - 10;
б) - 65 : 13 + 90 : (-15);
в) (7 - 10) · (-18) + 42 : (-7);
г) 15 - (4 + 8 : (- 2)) - 6;
д) 0,2 - 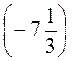 : 11;
: 11;
есть) -4 : 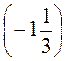 - 10 : (-20).
- 10 : (-20).
2. Найдите значение выражения 12 : х - 4,6, если: х = -3; -1,5; 4; -0,5.
3. Решите уравнение:
a) -2x = 10; б) -3x = -9; в) 0,2x = -4; г) -1,2x = 3,6; д) -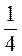 x =
x =  ; е) -
; е) -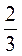 х = -1
х = -1 .
.
4. Решите уравнение: а) 4х = -10; б) -0,4 х = -2; в) 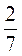 х = -
х = -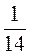 .
.
5. Решите уравнение:
а) 3(2х - 11) = -21; б) -2(5 - 2х) = -14; в) -5(х + 3) + 3 = -17.
6. Дополнительные упражнения
Задача 1. Найдите корень уравнения:
a) (2,5 в- 0,75) · (-0,3) = 0;
б) (-0,01 х - 4,9) · 54,2 = 0;
в) 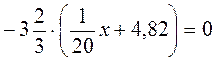 ;
;
г) 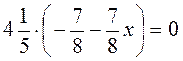 .
.
Задание 2. Найдите неизвестный член пропорции:
а) 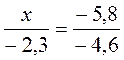 ; б)
; б) 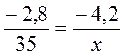 ; в)
; в) 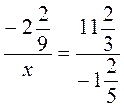 ; г)
; г) 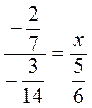 .
.
@ Можно заметить, что знак «·» в этих уравнениях (то есть значение выражения a·b:c, где a, b, c - рациональные числа) так же зависит от количества отрицательных чисел, как и знак произведения!
Логическое упражнение. Задача 3. а) выражение пропущено?
б) Какое число пропущено?
5х - 3 = 42 |
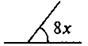
|
108° |
5 + 3х = 26 |

|
? |
IV. Итоги урока
Повторяем правила и свойства деления рациональных чисел.
V. Домашнее задание
1. Вычислите: а) -42 : 14 - 18 : (-2); б) -60 : 12 + (-2 - 8) · 5; в) -4 : (-9).
: (-9).
2. Решите уравнения: а) -3(3х + 1) = 15; б) 2 + 3(х - 3) = -13.
3. Выполните действия: а) -18 : (-3 + 2,7) + 9; б) (-2)3 : 4 + (-0,8) : (-0,04); в) 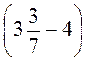 : (-4).
: (-4).
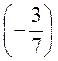
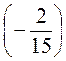
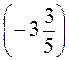 :
: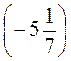 :
: .
.