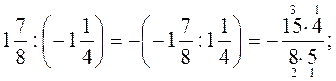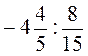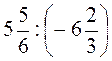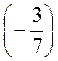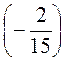Урок № 89
Тема. Деление рациональных чисел
Цель: основываясь на знаниях учащихся о содержании действия деления и правила умножения рациональных чисел, сформулировать правила деления рациональных чисел, начать работу по выработке умений применять эти правила при решении упражнений, предполагающих выполнение деления рациональных чисел.
Тип урока: усвоение новых знаний.
Ход урока
I. Проверка домашнего задания
Собираем тетради на проверку.
II. Актуализация опорных знаний
Вопрос к классу
1. Как называются числа а, b, с в равенства а · b = с? Как найти а, если b и c известны?
2. Чему равны произведения -3 · (-5); 3 · 5; -3 · 5; 3 · (-5)?
3. Как называются числа a, b, с в записи: a : b = c? Как проверить правильность выполнения деления?
4. Вместо * поставьте такие числа, чтобы равенство было правильным: 3,97 · * = 3,97; 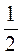 · * = 0; 0 · * = 0; 0 · * = 1
· * = 0; 0 · * = 0; 0 · * = 1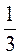 .
.
III. Формирование знаний
@ Можно изложение нового материала разбить на два урока: по аналогии, как были рассмотрены вопросы сложения и умножения рациональных чисел - на первом уроке мы выводили правило деления двух рациональных чисел с одинаковыми знаками, на втором - деление чисел с разными знаками. Если же правила умножения рациональных чисел разработаны учащимися на достаточном уровне, можно дать на первом уроке темы правила и свойства деления рациональных чисел (т.е. весь теоретический материал), а второй и третий уроки темы (уроки № 94, 95) полностью посвятить отработке навыков использования названных выше правил.
1. Смысл деления рациональных чисел
Задача 1. Неизвестное число умножили на -3, получили 15. Какое неизвестное число?
Решения. Очевидно, что условие задачи на язык математики записывают так: если х - неизвестное число, то x · (-3) = 15; понятно, что x = 15 : (-3).
Итак, разделить какое-то а на b значит найти такое с, чтобы a = b · c.
2. Деление двух чисел с одинаковыми знаками
Мы знаем, что -3 · (+5) = -15; -3 · (-5) = + 15, и чтобы умножить два числа с одинаковыми знаками (разными знаками), достаточно перемножить их модули и перед результатом поставить знак «+» («-»).
Но если -3 · (+5) = -15, то -15 : (+5) = -3; -15 : (-3) = +5;
или -15 : (+5) = -(|-15| : |+5|) = -(15 : 5) = -3;
и -15 : (-3) = +(|-15| : |-3|) = +(15 : 3) = +5.
Нетрудно заметить, что во время деления рациональных чисел с одинаковыми (разными) знаками достаточно разделить модуль делимого на модуль делителя и перед результатом поставить знак «+» («-»).
(Обычно сначала определяют знак доли, а затем уже выполняют деление модулей.)
Например
а) 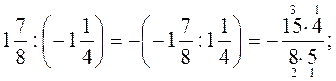
б) -25,116 : (-3,12) = 25,116 : 3,12 = 2511,6 : 312 = 8,05.
@ Важно подчеркнуть, что есть определенная аналогия между правилами умножения и деления рациональных чисел (это поможет учащимся быстрее запомнить эти правила).
3. Свойства деления
Мы уже знаем, что а·1 = а; а · 0 = 0, следовательно, из содержания деления следует: а : 1 = а, а : а = 1, 0 : а = 0, если а ≠ 0, но а : 0 нельзя ни при каких а (если у учащихся возникнут вопросы «почему?», можно повторить объяснения, которыми пользовались во время изучения темы «Деление натуральных чисел» в 5 классе).
IV. Формирование умений
Устные упражнения
1. Прочитайте равенства, назовите компоненты действий. Правильно ли выполнено деление рациональных чисел?
а) (-36) : (-12) = -3; б) -36 : (+12) = -3; в) (-36) : (-12) = +3; г) -36 : (-12) = + .
.
2. Какой знак имеет доля?
а) -18 : (-12); б) -99 : 12; в) +40 : (-1).
3. Вычислите: а) (-40): (-2); б) -125 : 5; в) 0 : (-51); г) 203 : (-10); д) -56 : 14; ж) 80 : (-16); ж) -90 : (-15); с) -25,3 : 0,1.
Письменные упражнения
1. Найдите долю:
а) - 4,5 : 9; б) - 5 : (- 0,5); в) 38,6 : (- 3,86); г) - 9,6 : (- 4,8); д) - 5,2 : 0,01; есть) - 340 : (- 1,7); ж) - 6,6 : (- 1,1); с) 14: (-0,28); и) - 350 : 1,75.
2. Найдите долю:
а) 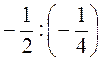 ; б)
; б) 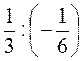 ; в)
; в) 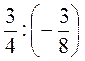 ; г) -3 : 1
; г) -3 : 1 ; д)
; д) 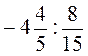 ; е)
; е) 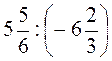 .
.
3. Решите уравнение: а) -2х = 10; б) -3х = -9; в) 0,2 х = -4; г) -1,2 х = 3,6; д) -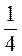 х =
х =  ; е) -
; е) -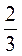 х = -1
х = -1 .
.
Дополнительные упражнения
1. Упростите выражение и вычислите его значение:
а) -5а - 8а + 8a при а = -5; -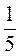 ; -2,6; 1.
; -2,6; 1.
б) 7b - 15b + 17b - 10b при b = -1; 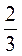 ; -15,5; 0.
; -15,5; 0.
2. Найдите значение выражения abc наиболее удобным способом при данных значениях букв:
а |
b |
с |
19,19 |
0,25 |
- 4 |
5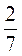 |
-9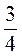 |
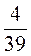
|
-40 |
0,801 |
2,5 |
3. Решите уравнения: а) х · (-8,8) = 0; б) (-x) · 3,74 = 0; в) (х - 15) · 5,3 = 0; г) (2,3 + x) · (-7,2) = 0; д) -7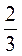 · (х + 9,11) = 0; е) 92,1 · (-89,89 - х) = 0.
· (х + 9,11) = 0; е) 92,1 · (-89,89 - х) = 0.
4. а) количество отрицательных множителей должна быть в произведении, чтобы он выражался положительным числом? отрицательным числом?
б) При каких условиях произведение нескольких множителей равно 0?
в) Как изменится произведение нескольких чисел, если его умножить на (-1)?
V. Итоги урока
Вопрос к классу
По какому правилу выполняем деление двух чисел:
а) с одинаковыми знаками;
б) с разными знаками;
в) положительного на отрицательное;
г) отрицательного на -3?
VI. Домашнее задание
Устные упражнения
1. Какой знак имеет доля: а) - 18 : (- 12); б) - 99 : 12; в) 40 : (- 32)?
2. Правильно ли выполнено деление?
а) -48 : 6 = -8; б) 0,9 : (-1) = 0,9; в) -4,5 : (- 1,5) = -3?
3. Вычислите: а) (- 40) : (- 2); б) - 125 : 5; в) 0 : (- 51); г) 203 : (- 10); д) - 56 : 14; ж) 80: (- 16); ж) - 90 : (- 15); с) - 25,3 : 0,1.
Письменные упражнения
1. Найдите долю.
а) 3,6: (-4); б) 2,5 : (-7,5); в) - 8,64 : 1,2; г) - 56,68 : (-0,01); д) -2 : 0,05; е) -3: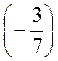 ; ж)
; ж) 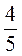 :
: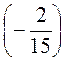 ;)
;) 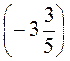 :
: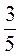 ; ы)
; ы) 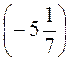 :
: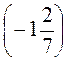 .
.
2. Решите уравнения: а) 4x = -10; б) -0,4 х = -2; в) 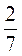 х = -
х = -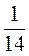 .
.
3. Найдите значение выражения:
а) -5(1,2а - 6) + 7а, если a = -208;
б) (5а - 0,8) - (-5,2a + 0,1), если а = 0,1.