Урок № 87
Тема. Распределительная свойство умножения. Возведение подобных слагаемых
Цель: используя знания о способах использования распределительного свойства умножения, выработать умения:
а) находить подобные слагаемые и определять по алгебраической суммы их коэффициенты;
б) выполнять возведение подобных слагаемых.
Тип урока: применение знаний, умений и навыков.
Ход урока
I. Проверка домашнего задания
Математический диктант
Вариант 1 [2]
1. Запишите выражение и вычислите его значение:
577 · 58 + 423 · 58 [76,8 · 9,5 - 66,8 · 9,5];
34,2 · 91,3 - 24,2 · 91,3 [718 · 34 + 282 · 34].
2. Запишите выражение и вычислите его значение: 6 · 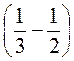
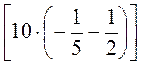 .
.
3. Подав один из множителей в виде суммы разрядных единицы и числа ±1, вычислите устно значение произведения -999 · 17 [-12 · 9999].
II. Актуализация опорных знаний
Во время проверки правильности решения задач математического диктанта учащиеся повторяют сами формулировки распределительной свойства и способы ее применения (для раскрытия скобок и вынесения общего множителя за скобки).
Обратившись к конспекту, записанного на предыдущем уроке, учащиеся понимают, что основным материалом урока является работа с буквенными выражениями.
III. Дополнение знаний
Чтобы иметь четкие представления о содержании понятий «подобные слагаемые» и «возведение подобных слагаемых», мы формулируем соответствующие определения и показываем на примерах их содержание.
IV. Выработка умений
@ Обратим внимание на такие моменты:
а) чтобы свести подобные слагаемые, надо правильно определить их коэффициенты (а для этого вспоминаем о алгебраическую сумму), а потом уже добавлять эти коэффициенты; во время возведения подобных слагаемых буквенная часть не изменяется;
б) в выражении может быть не одна, а несколько групп подобных слагаемых. В этом случае сначала отдельно выделяем каждую группу (традиционно подчеркиваем определенным количеством рисок каждую группу подобных слагаемых), а потом уже для каждой группы подобных слагаемых повторяем п. а);
в) если данное выражение содержит скобки, то прежде чем свести подобные слагаемые (т.е. выполнить сложение), надо раскрыть скобки (т.е. выполнить умножение, используя распределительную свойство, или правила), а потом уже смотри п. а) или б);
г) если в алгебраической сумме есть несколько (больше одного) числовых слагаемых, то их также можно считать подобными слагаемыми (и не забывайте их добавлять).
Устные упражнения
Сведите подобные слагаемые в выражении: а) 5х - 4х; б) 4а - а; в) 5х - 7х; г) 4а - 5а + а.
Письменные упражнения
1. Сведите подобные слагаемые:
а) 9a - 13a + 2a;
б) 5a - 6a + 2a - 10a;
в) -9х + 7х - 5х + 2х;
г) 2,8b - b + 2,8b - b;
д) -4х - 7 - 5х + 10х;
e) 5a + b - 7b + 3a;
же) -7а + 5а - х - 6х;
с) 12х - 11 + 4а - 7х;
ы) 8а - 9х + 4 - а + х.
Записи в тетрадях могут иметь такой вид:
а) 9а - 13а + 2а = (9 - 13 + 2) а = -2а;
б) 5a + b - 7b + 3a = (5 + 3)a + (1 - 7)b = 8a + (-6)b = 8a - 6b i т. д.
2. Раскройте скобки:
а) (х - у) · 5;
б) (а + b - с) · 4;
в) (2х - у) · (-3);
г) -2a(b + 2с - 3m);
д) -a(6b - 5c);
е) (а + 3b + с)(-2х).
3. Упростите выражение:
а) 3(-2х + 5) + 4(х - 2);
б) -(2а - 3) - 2(3а - 1);
в) -5(-3х + 2) - (9 - х);
г) (3b - 1) · (-5) + (4 + b) · (-2).
4. Упростите выражение:
а) 0,7 х 0,9 х + 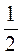 х;
х;
б) -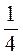 b + 1
b + 1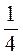 b -
b - 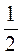 b;
b;
в) 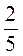 а +
а + 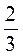 b - b + 0,4a;
b - b + 0,4a;
г) -7(а - 2b + 2) + (5а - 5) · (-2);
д) а(3х - 2у + 5) - 2а(-2х - у);
есть) -6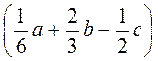 + 4а + 7b.
+ 4а + 7b.
Дополнительные упражнения
1. Один рабочий может выполнить заказ за 6 дней, а второй - за 15 дней. Сначала 2 дня над заказом работал первый рабочий, а затем закончил второй. Сколько дней работал второй рабочий?
2. Найдите значение выражения:
а) (3х)2, если х = 2; -2;
б) а3 - 12, если а = -2; 3.
IV. Итоги урока
Заполните пропуски:
а) 5a - 3a = ...;
б) 5a - 3a + b = ...;
в) 5a - 3a + b - 2b = ...;
г) 5(a + b) - 3a = ..;
д) 5(a + b) - (a - b) = ...
VI. Домашнее задание
Устные упражнения
1. Назовите подобные слагаемые в выражениях:
а) х - 2у + 3х - у;
б) 7b - a - 2ab + b - 3ab.
2. Сведите подобные слагаемые: а) 5х - 4х; б) 4а - а; в) 5х - 7х; г) 4а - 5а + а.
3. Письменные упражнения
1. Раскройте скобки: а) 3(а - с); б) -6(2а + b); в) (-4а - 3b) · 5; г) а(3b - 4с); д) (x + y - z) · (-a); e) -5a(-2b + 4c - d).
2. Сведите подобные слагаемые:
а) 3с + 7с - 8с;
б) 16а - 5а + 7а - 11а;
в) -4t + 3t - 8 - 7t;
г) 8x - 8y + 2y - 6x;
д) 4,5 a - 7b - 1,5 a + 1;
e) -a + 3b - 4b + 1,5 a.
3. Упростите выражение: а) (5х - 3) · 2 - 5(3 - 2х); б) (3а - 2) + 5(а - 2).
4. Один экскаватор может вырыть траншею за 9 ч, а второй эту же траншею - за 6 ч. Какую часть траншеи выроют экскаваторы за 3 ч совместной работы?