Урок № 86
Тема. Распределительная свойство умножения
Цель: повторить рассмотрены в 5 классе способы записи и применение распределительного свойства умножения и распространить ее на умножение рациональных чисел.
Тип урока: систематизация и обобщение знаний.
Ход урока
I. Проверка домашнего задания
Выборочно проверяем тетради.
Устные упражнения (фронтально)
1. Вычислите:
а) 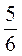 +
+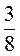 ; б)
; б) 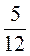 -
- 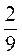 ; в) 2
; в) 2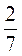 - 1
- 1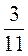 ; г) 3
; г) 3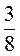 + 1
+ 1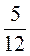 ; д)
; д) 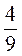 ·
· 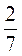 ; е)
; е) 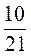 ·
· 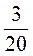 ; ж) 4
; ж) 4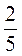 · 5; с) 4
· 5; с) 4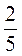 · 10; к)
· 10; к) 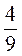 :
: 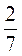 ; л)
; л) 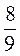 :
: 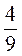 ; г) 0 : 4
; г) 0 : 4 ; н) 1 : 1
; н) 1 : 1 .
.
2. Назовите коэффициент выражений: 3ху; -в; -1,2 а; - b · 3c; m; -2abc ·
b · 3c; m; -2abc ·  b.
b.
3. Чему равно произведение всех целых чисел от -299 до 300 включительно?
4. Не вычисляя, сравните произведения: -33 · 50 и -11 · 150; -45 · 13 и -26 · 22.
II. Актуализация опорных знаний
1. Как вычислить удобным способом значение выражения: а) 39 · 10 + 10 · 21; б) 45 : 13,5 - 45 · 12,5; в) 4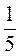 · 5?
· 5?
2. Среди представленных выражений найдите пары равных: а) 5а + 3а; б) 5 · (а + b); в) 3а - а; г) 8; д) 2а; в) 5а + 5b; ж) 15а2; с) 5а - 3а.
3. Назовите слагаемые в сумме -3 + a - 5m - 12 · (-3).
III. Систематизация и обобщение знаний
@ После выполнения задания 1 и задания 2 учащиеся «догадываются», что речь на уроке пойдет об использование распределительного свойства умножения (учащиеся должны иметь представление об этом свойстве и способы ее использования с 5 класса) для умножения рациональных чисел. Поэтому задачей учителя является не столько объяснение нового материала, сколько обобщение и систематизация знаний учащихся по этому вопросу. Аналогично рассмотренному вопросу «Соединительная и переставная свойства умножения» мы работаем над тем, чтобы учащиеся осознали, что:
1) распределительная свойство используется для любых рациональных чисел;
2) распределительная свойство используется в прямом (раскрытие скобок) и обратном (вынесение общего множителя за скобки) порядке;
3) распределительная свойство умножения используется как для упрощения вычислений, так и для упрощения выражений (возведение подобных слагаемых). Чтобы ученики имели такие систематизированные представления о распределительную свойство умножения и его применение, можно сопроводить объяснение записями в виде конспекта 34, которые ученики дублируют в рабочих тетрадях:
Конспект 34 |
Распределительная свойство умножения |
1. Раскрытие скобок:
a(b + c) = ab + ас.
2. Вынесение общего множителя за скобки:
ab + ас = а(b + с) |
Пример
1. а) -5(а + 0,3) = (-5) · а + (-5) · 0,3 = -5а + (-1,5) = -5a - 1,5;
б) - 4 · 9 = · 9 = 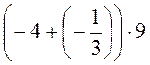 = (-4) · 9 + = (-4) · 9 + 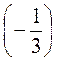 · 9 = -36 + (-3) = -39. · 9 = -36 + (-3) = -39.
2. а) 4 · (-3) + 4 · 7 = 4 · (-3 + 7) = 4 · 4 = 16;
б) 5х - 4х = х(5 - 4) = х · 1 = х. |
IV. Совершенствование умений, отработка навыков
@ Поскольку на изучение темы программой отводится 3 часа, автор считает целесообразным разделить учебный материал на две части: на этом уроке занимаемся вычислениями (работа с числовыми выражениями), на следующем - работа с буквенными выражениями; на третьем - обобщаем материал, пишем самостоятельную работу.
Устные упражнения
1. Вычислите: а) 21 · 3 - 31 · 3; б) 27 · 25 - 17 · 2,5; в) 25 · (-9) + 5 · (-9); г) 54 · (-8) + 54 · 9; д) 25 · 90 +25 · (-86); е) +3 · 3; ж) -3
· 3; ж) -3 · (-9).
· (-9).
2. Прочитайте выражение, используя слова «сумма», «произведение»: -3 · 2 + 3 · 7; -0,3 · 0,2 + 0,1 · (-0,7); -3,4 - 5,4.
Письменные упражнения
Вычислите:
1. а) 54 · 4 - 14 · 54;
б) -17 · 25 - 5 · (- 17);
в) 2,7 · 19 - 3,7 · 19;
г) 91 · 31 - 32 · 91 + 91;
д) 1,4 · 1,9 - 3,2 · 1,4 - 1,4 · 8,7;
есть) -5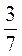 ·
· 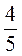 -
- 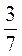 ·
· 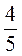 ;
;
ж) 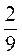 ·
· 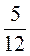 -
- 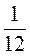 ·
· 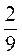 -
-  ·
· 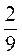 .
.
2. а) 6 · 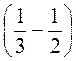 ; б)
; б) 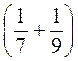 · (-63); в) 12 ·
· (-63); в) 12 · 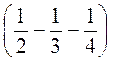 .
.
3. Вынесите за скобки общий множитель и выполните действия: а) 15 · 19 + 30 · 3; б) 90 · 7 - 60 · 8; в) 50 · 17 + 25 · 3.
4. Вычислите, используя распределительную свойство умножения: а) -23 · (- 99); б) 98 · (-11); в) 999 · (- 17).
5. Вычислите рационально:
а) 78 · 62 + 13 · 78 - 75 · 68;
б) 54 · 36 - 42 · 54 + 6 · 74;
в) 478 · 27 + 28 · 478 - 678 · 55;
г) 4,8 · 6,5 - 8,5 · 6,8 + 2 · 4,8.
@ Задача 1. Особое внимание обращаем на то, что, прежде чем выносить общий множитель за скобки, надо понять, какие слагаемые записаны (то есть отрабатываем понятия «алгебраическая сумма»).
@ Задание 2. Снова в скобках имеем алгебраическую сумму, а поэтому учитываем это во время умножения.
Например
а) 6 · 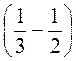 = 6 ·
= 6 · 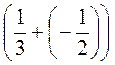 = 6 ·
= 6 ·  + 6 ·
+ 6 · 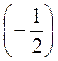 = 2 + (-3) = -1 и т. д.
= 2 + (-3) = -1 и т. д.
Задача 3. Упражнение является подготовительной для выработки представления о общий множитель как наибольший общий делитель слагаемых.
Задача 4. Учимся использовать приемы быстрого счета - подаем один из слагаемых как алгебраическую сумму разрядной единицы и числа ±1.
Задание 5. Последовательное неоднократное использование распределительной свойства.
V. Итог урока
Еще раз напоминаем ученикам (после решения № 4 и № 5 это очень наглядно), что использование распределительного свойства умножения позволяет во многих случаях достаточно сложные действия делать устно.
VI. Домашнее задание
1. Поставьте вместо звездочки знак «» или «>»так, чтобы образовалась правильная неравенство: а) -7,2 · (-15) * 100; б) 100 · (- 3) * 300; в) 0,2 · (-14) * -2,5.
2. Вычислите рационально: а) 36 · 28 + 36 · 39 - 67 · 46; б) 3,4 · 4,5 - 3,4 · 10,6 + 6,1 · 4,4.
3. Выполните действия: а) 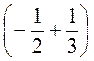 · (-6); б)
· (-6); б) 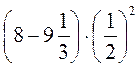 .
.
Дополнительная упражнение
Как вычислить устно: 11 · 99; (-11) · (-273); 99 · (-273)?
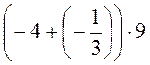
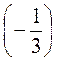
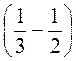
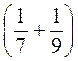 ·
·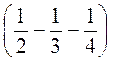 .
.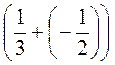
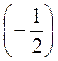
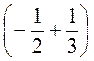 ·
· 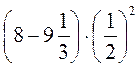 .
.