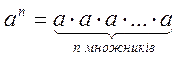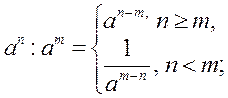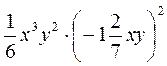Урок № 83
Тема. Повторение и систематизация материала, изученного в 7 классе. Преобразование выражений
Цель: повторить и систематизировать знания о видах и способах преобразования буквенных выражений, изученных в 7 классе; повторить и усовершенствовать умения использовать приобретенные знания при решении типовых упражнений.
Тип урока: повторение и систематизация знаний, умений, навыков.
Ход урока
I. Организационный момент
1. Проверка готовности к уроку.
2. План работы на уроке.
Результаты выполнения тематической контрольной работы № 8.
II. Проверка домашнего задания
@ Собираем тетради с анализом ошибок и коррекцией (выполненные самостоятельно аналогичные задачи другого варианта).
III. Формулировка цели и задач урока
@ Главная дидактическая цель этого и последующих двух уроков - повторить и систематизировать знания и навыки, приобретенные во время изучения курса алгебры в 7 классе.
IV. Повторение и систематизация знаний учащихся
@ Поскольку времени на повторение учебного материала маловато, работу по систематизации и обобщения организуем за тремя основными содержательными линиями: 1) выражения их преобразования; 2) уравнения, системы уравнений и их применение; 3) функции и графики.
Именно на этом уроке мы и работаем с первой содержательной линией «Выражения и их преобразования».
Для того чтобы этот этап урока был самым эффективным, учитель заготавливает таблицы и схемы, отражающие основные знания по теме и логические связи между ними:
Схема 1
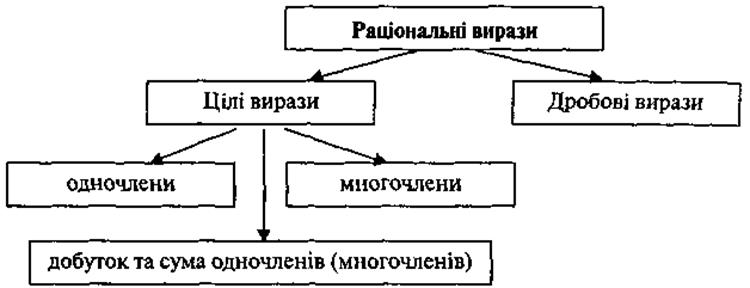
Схема 2

Схема 3
Степень с натуральным показателем |
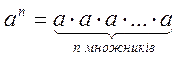
|
а - основа
n - показатель
аn - степень |
аn · аm = аn+m; 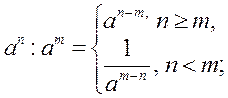 (аm)n = аmn; (аb)n = аnbn. (аm)n = аmn; (аb)n = аnbn. |
Схема 4
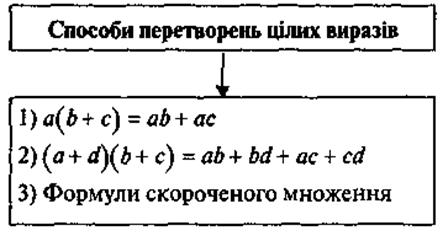
V. Повторение и систематизация способов действий
Выполнение письменных упражнений
1. Упростите выражение:
1) 8х2 · ху;
2) -3а2b · 2(а5)2;
3) 0,5 ас · (-4а3с)2 · а2с;
4) (х3)3n · (х5хn+1)2;
5) 4а(а2 - 4а + 3);
6) (4ab2 + 9a2)(2b2 - 3а);
7) (2b - 9)(2b + 9) - 4b2;
8) (а + 3)(а2 - 3а + 9) - 27;
9) (4у - 5у2)2 + (2у + 5у2)2 - 20у2.
2. Разложите на множители:
1) а2 - 2а;
2) ах - ау + 3х - 3у;
3) 9n2 - 4m2;
4) 120 - 30а4;
5) 27х3 + 0,008у3;
6) а2 + 8а + 16;
7) 6х2 - 24ху + 24у2;
8) а4 - 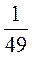 а2;
а2;
9) a2 - 4b2 + 2b + 4;
10) х2 - 4xв + 4у2 - 4y4;
11) х3 - (m - n)3; 12) х2 - 2х - 3.
3. Докажите, что значение выражения:
а) 97 - 312 делится на 8;
б) (x + 1)2 - (х - 1)(х + 3) не зависит от значения х;
в) (2n + 3)2 - (2n - 1)2 при любом целом значении п делится на 8.
VI. Итоги урока. Контрольное задание
Вариант 1 |
Вариант 2 |
1. Упростите выражение:
1) 5ху3 · (-2х2в)4;
2) (2у - 3x)2 - (3х + 2у)(2у - 3х).
2. Разложите на множители.
1) 4аb3 - a3b;
2) -9b - 6b2 - b3;
3) 27а2 - a5;
4) а2 + 2аb + b2 - 9 |
1. Упростите выражение:
1) 10x2у · (-3ху2)3;
2) (х + 4в)2 - (4у - х)(х + 4у).
2. Разложите на множители:
1) ab3 - 9a3b;
б) -25а + 10a2 - a3;
3) х4 - 125х;
4) а2 + 4аb + 4b2 - 9 |
VII. Домашнее задание
№ 1. Повторите правила выполнения действий с одночленами, многочленами.
№ 2. Упростите выражение:
1) 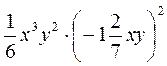 ;
;
2) 3x2 - 6x + x2 - 3 + x;
3) 8a2 + 4a - 3 - (7 - 8a + 3a2);
4) (2х2 - 4х + 8) · (-0,5х2);
5) (5х - 2у)(5х + 2у);
6) (10 - 3m)(2 + 3m) + (5m - 4)(5 - 2m);
7) (n - 1)(n2 + n + 1) - n3.
№ 3. Разложите на множители:
1) 2х + 2ху;
2) х2у - 2х + ху - 2;
3) х2 - 2ху + у2;
4) а2 + 3a - 4.
№ 4. Повторите и выпишите названия основных понятий, связанных с понятием уравнения (7 класс).