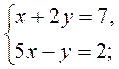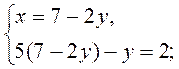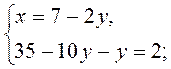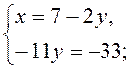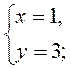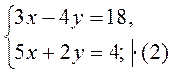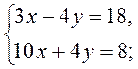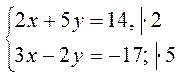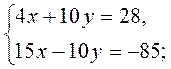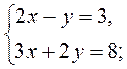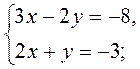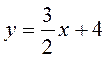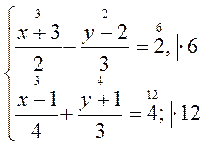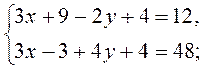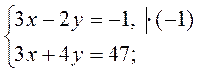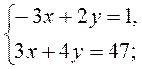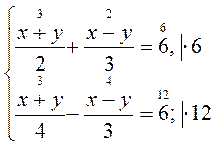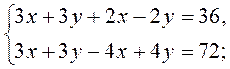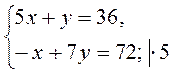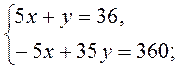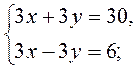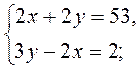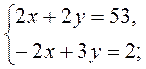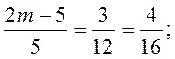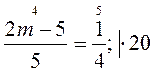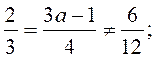5*. Пусть х (км/ч) - скорость первого пешехода, а в (км/ч) - скорость второго пешехода. Тогда за 3 часа первый пешеход пройдет 3х (км), а второй - 3у (км). А вместе за 3 часа они преодолеют 30 км, т.е. 3х + 3у = 30, причем первый пешеход преодолел на 6 км больше второго, следовательно, 3х - 3у = 6.
Составим и решим систему уравнений:
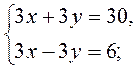 
2х = 12; х = 6;
в =10 - 6 = 4.
Итак, скорость первого пешехода 6 км/ч., а второго - 4 км/ч.
Ответ. 6 км/ч., 4 км/ч. |
5*. Пусть скорость первого велосипедиста х (км/ч). а второго в (км/ч). тогда за 2 часа до встречи первый преодолел 2х (км), а второй - 2у (км), а вместе 53 км. Значит, 2х + 2у = 53. Поскольку второй за 3 часа преодолевает 3у (км), а первый за 2 ч. - 2х (км), причем второй преодолеет на 18 км больше, то имеем: 3у - 2х = 2.
Составим и решим систему уравнений:
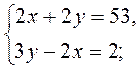 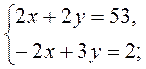
5у = 55; в =11;
2х + 22 = 53; 2х = 31; х = 15,5.
Итак, скорость первого велосипедиста 15,5 км/ч., а второго - 11 км/ч.
Ответ. 15,5 км/ч., 11 км/ч. |
6**. Система линейных уравнений имеет множество решений, если одноименные коэффициенты пропорциональны:
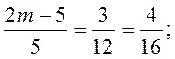 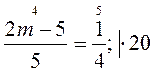
8m - 20 = 5; 8m = 25; m = 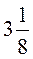 . .
Ответ. 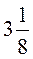 . . |
6**. Система линейных уравнений не имеет решений, если коэффициенты при х и у пропорциональны, но их отношение не равно отношению свободных членов, то есть 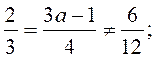
9а - 3 = 8; a = 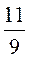 ; ;
6a - 2 ≠ 4; 6а ≠ 8; а ≠ 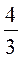 . .
Ответ. a = 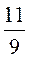 . . |
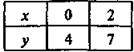
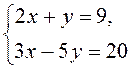 методом подстановки.
методом подстановки.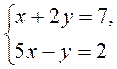 методом подстановки.
методом подстановки.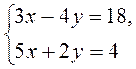 методом сложения.
методом сложения.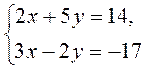 методом сложения.
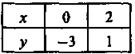
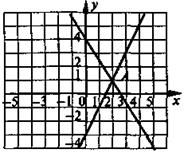
методом сложения.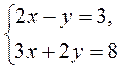 графически.
графически.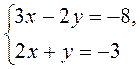 графически.
графически.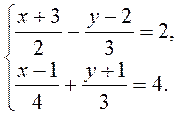
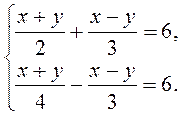
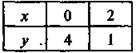
 имеет множество решений?
имеет множество решений?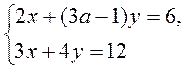 не имеет решений?
не имеет решений?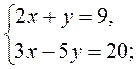
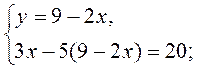
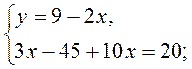
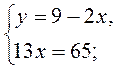
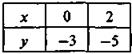
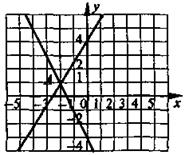
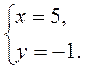 Ответ. (5; -1).
Ответ. (5; -1).