Урок № 81
Тема. Системы линейных уравнений с двумя переменными
Цель: повторить и систематизировать знания учащихся о содержании основных понятий темы «Системы линейных уравнений с двумя переменными»; повторить и систематизировать умения и способы действий, которыми овладели учащиеся при решении типовых задач, предусмотренных программой по математике; подготовить учащихся к тематическому оцениванию.
Тип урока: повторение и систематизация знаний, умений, навыков.
Ход урока
И. Организационный момент
1. Проверка готовности к уроку.
2. Определение места урока в теме.
II. Проверка домашнего задания
@ Выполнению задания № 2 (1; 2) проверяем, собрав тетради учащихся; работу можно оценить как домашнюю самостоятельную работу; после сбора тетрадей, можно осветить самый сложный момент решения (№ 2 (2) - составления второго уравнения упрощается, если 30 мин. выразить как 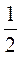 или 0,5 часов).
или 0,5 часов).
III. Формулировка цели и задач урока
@ Поскольку этот урок - предпоследний в теме, то логично, что его основная дидактическая цель - систематизировать знания и умения учащихся, приобретенные в ходе изучения темы, то есть надлежащая подготовка к тематическому оцениванию.
@ Используя выполненное домашнее задание № 1 (см. предыдущее домашнее задание), организуем и проводим мини-викторину или игровой момент «самый Умный» (ответы нескольких учеников на заранее подготовленные вопросы учителя по разделам: «Уравнение с двумя переменными и их решения», «Применение систем линейных уравнений с двумя переменными»).
Итогом этого этапа урока должно быть сознательное понимание учащимися смысла основных понятий и логической связи между ними.
IV. Повторение и систематизация умений и способов действий
@ Предлагаем учащимся решить типичные задачи из названных подразделов разного уровня сложности.
Важнейшие условия, которые нужно выполнить:
1) как можно больше самостоятельности учащихся во время выполнения заданий (идеальный вариант - сначала предлагаем задания для самостоятельной проработки, а затем - презентация выполненных заданий);
2) обязательная коррекция после выполнения каждого блока заданий.
Выполнение письменных упражнений
И базовый уровень. Тестовые задания
1. Укажите решение уравнения х - у = 2:
1) (3; 2); 2) (3; 1); 3) (5; 2); 4) (-3; -2).
2. Какая из пар является решением системы уравнений 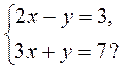
1) (3; 3); 2) (2; 2); 3) (2; 1); 4) (-1; -5).
3. Решите систему уравнений 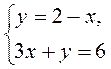 способом подстановки и укажите правильный ответ:
способом подстановки и укажите правильный ответ:
1) (1; 1); 2) (0; 2); 3) (2; 0); 4) (4; -2).
4. Решите систему уравнений 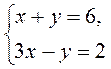 способом сложения и укажите правильный ответ:
способом сложения и укажите правильный ответ:
1) (-2; 8); 2) (2; 4); 3) (4; 2); 4) (-4; 10).
5. Сумма двух чисел равна 1, причем одно из них на 5 больше второго. Пусть больше число равно х, а меньше в. Какая система уравнений соответствует условию задачи?
1) 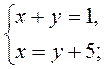 2)
2) 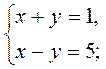 3)
3) 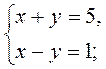 4)
4) 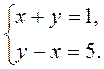
II уровень
1. Решите графически систему уравнений 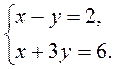
2. Решите систему уравнений:
1) 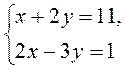 способом подстановки;
способом подстановки;
2) 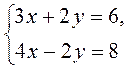 способом сложения;
способом сложения;
3) 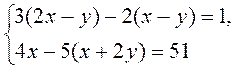 любым удобным способом.
любым удобным способом.
3. Решите задачу, составив систему уравнений.
Общая масса малой и великой деталей 320 г, а две большие и три малые детали имеют общую массу 760 кг. Какова масса каждой детали?
III уровень
1. Найдите такое число а, чтобы график уравнения 2х - ау = 2 проходил через точку (-1; 2).
2. Найдите такие числа а и b, чтобы график уравнение 2ах - (b + 2)у = 2 проходил через точки (-1; 4) и (2; 2).
3. При каком значении коэффициента а система 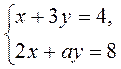 имеет множество решений?
имеет множество решений?
VI. Итоги урока
Можно подвести, проанализировав качество самостоятельной работы учащихся (собрать тетради или, если ученики работали с листами-заданиями,- собрать задания). Желательно побудить учащихся к самоанализу - каждый оставляет себе условие предложенных заданий и дома дорабатывает то, что не получилось в классе.
VII. Домашнее задание
Домашняя контрольная работа
№ 1. Проанализируйте и исправьте ошибки, допущенные в классной работе.
№ 2. Постройте график уравнения:
1) х - 2у = 4; 2) 4х + у = -4; 3) 3х - 2у = 6.
№ 3. Найдите координаты точек пересечения графиков уравнений 2х - 3у = 1 и
х + 3у = 5, не выполняя построений.
№ 4. Решите систему уравнений:
1) 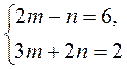 способом подстановки и способом сложения;
способом подстановки и способом сложения;
2) 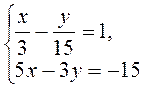 любым удобным для вас способом.
любым удобным для вас способом.
№5. Из пункта А В пункт В отправился велосипедист. Через 2 часа после этого из пункта В навстречу велосипедисту отправился пешеход и через 1 ч после своего выхода встретился с велосипедистом. Найдите скорость велосипедиста и скорость пешехода, если скорость велосипедиста на 8 км/ч больше скорости пешехода, а расстояние между пунктами А и В составляет 40 км.