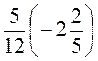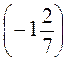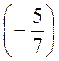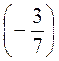Урок № 82
Тема. Умножение двух рациональных чисел с разными знаками
Цель: сформировать представление о содержании действия умножения двух рациональных чисел с разными знаками и выработать умение использовать этот алгоритм для вычисления значений выражений.
Тип урока: применение знаний, умений и навыков.
Ход урока
И. Проверка домашнего задания
1) Математический диктант
Вариант 1 [2]
1. Запишите в виде выражения произведение -3 и -4 [-5 и -7].
2. Выполните умножение:
а) -5 на -8 [-7-9];
б) -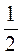 на -4 [-15 на -
на -4 [-15 на -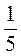 ];
];
в) -5,3 на -0,1 [-0,01 на -23].
3. Сравните произведения: -2,3 и -7,3 и 2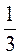 и 7
и 7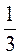 [-3
[-3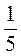 и -
и -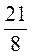 и 3,15 и +2,1].
и 3,15 и +2,1].
@ Во время проверки результатов выполнения математического диктанта повторяем правило умножения двух чисел с одинаковыми знаками.
II. Актуализация опорных знаний
Устные упражнения
1. Прочитайте выражения: а) 11·12; б) 11·12 + 5; в) 11·(12 + 5); г) 11·(12 - 5).
2. Вычислите: а) 10 · 15; б) 11 · 12; в) 24 · 5; г) 24 · 25; д) 25 · 16 (используя приемы быстрого счета).
3. Вместо * поставьте знак «>» или «», чтобы неравенство стало верным: а) -7 · (-3) * 0; б) -7 · (-3) * 10 · 2; в) -7 * 10 · 2.
III. Формирование знаний
Задача 1. Температура воздуха понижается каждый час на 2 °С. Сейчас термометр показывает 0 °С. Какую температуру воздуха будет показывать термометр через 3 ч?
Решения. Поскольку сейчас температура 0 °С, и каждый час она снижается на 2 °С, то через три часа она будет -2 + (-2) + (-2) = -6 градусов. Этот же результат можно было получить, обозначив почасовое снижение температуры -2 °С, а последующее время + 3 часа и выполнить действие: (-2) · (+3) = -6.
Итак, (-2) ∙ (+3) = -6. (1)
Задача 2. Сейчас температура воздуха 0 °С и ежечасно она повышается на 2 °С. Какую температуру показывал термометр 3 часа назад?
Решения. Поскольку сейчас 0 °С, и каждый час температура повышалась на 2 °С, то понятно, что три часа назад она была -6 °С. Этот же самый результат можем достать, обозначив щогодинну изменение температуры+2 °С, а время, что прошло, -3 ч (мы «возвращаемся» во времени назад). Тогда имеем: +2 · (-3) = -6. (2)
Можно рассмотреть несколько наглядных примеров, записать равенства, аналогичные (1) и (2), и сравнить их, получив такой вывод: Чтобы умножить два числа с одинаковыми знаками, надо:
1) перемножить их модули;
2) перед результатом поставить знак «-», то есть:
Произведение двух чисел с разными знаками есть число отрицательное; модуль этого числа равен произведению модулей данных чисел.
Например
а) -8 · (+5) = -(|-8| · |+5|) = - (8 · 5) = -40,
можно писать коротко (модули вычислять устно): -8 · (+5) = - (8 · 5) = -40;
б) +1,7 · (-5) = - (1,7 · 5) = -8,5.
Замечания. Во время умножения как сложения рациональных чисел сначала можно определять знак результата, а потом уже выполнять действия с модулями.
IV. Закрепления знаний. Выработка умений
Устные упражнения
1. Прочитайте равенства. Являются ли они правильными?
а) -3 · (-2) = -6; б) -3 · (+2) = +6; в) +3 · (-2) = -6; г) -(+3) · (-2) = 6.
2. Какой знак имеет произведение?
а) -3 · (-1,5); б) 9 · (107); в) - · 0,5; г) а · b, если а > 0, b 0?
· 0,5; г) а · b, если а > 0, b 0?
3. Вычислите: а) -4 · (-10); б) -7 · (+6); в) +8 · (+0,02); г) 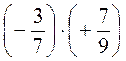 ; д)
; д) 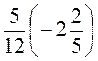 ; е) -0,01·(-0,1); ж) -0,1·(+9).
; е) -0,01·(-0,1); ж) -0,1·(+9).
Письменные упражнения
@ На этом уроке мы уже выполняем упражнения на умножение как чисел с одинаковыми знаками, так и чисел с разными знаками. Но, как и на предыдущем уроке, каждый раз требуем воспроизведения соответствующего алгоритма.
1. Выполните умножение: а) 11·72; б) -11 · (-72); в) -11 · 72; г) 11 · (-72). Обратить внимание на то, что, вычислив произведение модулей (в п. а), в следующих примерах мы должны только определить знак произведения и поставить его перед произведением модулей (повторяем алгоритм устного умножения двоцифрового числа 1).
2. Выполните умножение:
а) -16 · 2,5; б) 0,01 · (- 65); в) -100 · 0,02; г) -4 · (-10,5); д) -5 · 3 ; е)
; е) 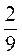 ·
·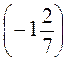 ; ж) -3
; ж) -3 ·
·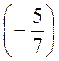 ; с) 5,6 ·
; с) 5,6 · 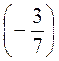 .
.
Перед выполнением действий требовать от учащихся анализа того, с каким именно случаем умножения имеем дело.
3. Вычислите: а) -16 + 8 · (-0,5); б) -2 · (-1,8 - 1,2); в) -8 · 0,5 + 5 · (-0,6); г) 5 ·
·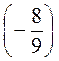 + 6; д) -
+ 6; д) - +
+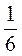 ·
·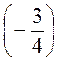 ; е)
; е)  ·
·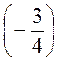 -
-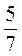 ·
·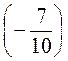 .
.
Перед выполнением действий требовать:
а) определить правильный порядок выполнения действий;
б) повторить алгоритмы умножения и сложения рациональных чисел.
4. Поставьте вместо звездочки знак «» или «>» так, чтобы образовалась правильная неравенство: а) 100 · (- 3) * 300; б) 0,2 · (-14) * -2,5.
Дополнительные упражнения
5. Вычислите:
а) (- 7,6 - 5,8 + 4,5) · (6,3 - 8,2);
б) -2,69 · (-0,8) + 0,7 · (4,3 - 7,8);
в) -10,8 · (-7,6 - 6,8) · (-3,5);
г) (- 7,65 · (- 0,4) - 5) · (3 - 1,02);
д) (- 2,36 + 6,82 - 5,45) · (46,5 - 91,5) + (- 45,09).
6. Вычислите: а) 5,6 · 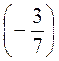 - (-5) · 3
- (-5) · 3 ; б) -0,75 ·
; б) -0,75 · 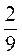 - 7
- 7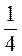 · (-0,3); в) (-3,4) ·
· (-0,3); в) (-3,4) · 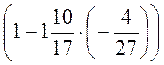 ; г)
; г) 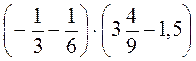 .
.
Более сложные задачи на совместные действия умножения и сложения рациональных чисел.
7. Логическое упражнение (на повторение)
Найдите и поставьте вместо (?) пропущенный рисунок:
V. Итог урока
1. Как выполнить умножение двух чисел, если они: а) с одинаковыми знаками, б) с разными знаками?
2. Что больше произведение двух чисел с одинаковыми знаками или произведение двух чисел с разными знаками?
3. Вместо * поставьте знаки «+» или «-», чтобы равенства стать правильными: а) *5 · *2 = -10; б) *5 · *2 = 10; в) (-5) · (-2) = *10.
VI. Домашнее задание
Устные упражнения
1. Вычислите а) 8 · 6; б) 8 · (- 6); в) -8 · 6; г) -8 · (-6); д) 7 · (-4); е) (-7) · (-4); ж) -5 · 4; с) -100 · 0.
2. Вычислите а) - 0,2 ·3; б) 2 · (-0,6); в) (-1,2) · (-2), г) -0,1 · (-20).
Письменные упражнения
1. Выполните умножение а) -12 · 25; б) 1,3 · (-5); в) -10 · (-70,1), г) -5,45 · (-1,02); д) 105 · (-0,18); е) 12 · 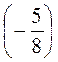 ;)
;)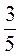 ·
· 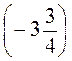 ; с) -4
; с) -4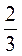 · 1
· 1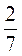 .
.
2. Вычислите а) - 0,4 · (-10) - 7; б) - 0,3 · 1,2 - 2,5; в) (0,1 - 0,6) · 8; г) -0,7 · 6 + 7,2 · 0,2, д) 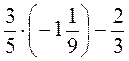 ; е)
; е) 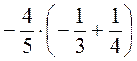 .
.
3. Вычислите 1,2 · (-6,39 + 4,84) - 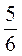 · 24,6.
· 24,6.
Упражнение на повторение
На первой книжной полке на 60 книг больше, чем на второй Сколько книг на каждой полке, если количество книг на второй полке составляет  количества всех книг?
количества всех книг?
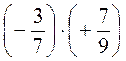 ; д)
; д)