Урок № 81
Тема. Умножение рациональных чисел с одинаковыми знаками
Цель: сформировать представление учащихся о содержании действия умножения рациональных чисел с одинаковыми знаками, закрепить знания соответствующего алгоритма, выработать умение его применения во время вычислений.
Оборудование: демонстрационный термометр.
Тип урока: усвоение новых знаний.
Ход урока
I. Проверка домашнего задания
В зависимости от того, каким образом был проведен урок-анализ тематической контрольной работы, мы или собираем домашние тетради с выполненной коррекцией знаний, или собираем творческие работы учащихся.
II. Актуализация опорных знаний
Устные упражнения
1. Вычислите:
а) 0,2 · 4; 2,1 · 3; 0,7 · 10; 0,5 · 2; 0,25 · 4;
б) 2,4 · 3; 3,02 · 7; 0,24 · 1000; 0,2 · 0,1; 2,7 · 100.
в)
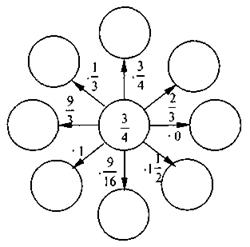
2. Запишите сумму в виде произведения:
а) 2 + 2 + 2;
б) 5 + 5 + 5 + 5;
в) 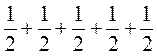 ;
;
г) 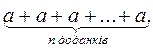
3. Вычислите сумму:
а) + 2 + (+2) + (+2);
б) -2 + (-2) + (-2);
в) 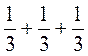 ;
;
г) 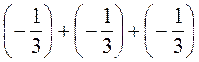 .
.
4. Найдите модули чисел:
а) -2; б) 5; в) -(-2,1); г) -5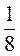 ; д) а, если а > 0; е) а, если а 0.
; д) а, если а > 0; е) а, если а 0.
5. Температура воздуха составляла +2 °С. Потом она: а) повысилась на 3 °С; б) снизилась на 3 °С.
Как найти новую температуру? (Запишите выражение.)
III. Формирование знаний
@ Как и на соответствующем уроке темы «Сложение и вычитание рациональных чисел», на этом уроке обращаемся к наглядных пособий, чтобы показать, как «работает» правило, а потом уже формулируем соответствующий алгоритм. Также автор считает целесообразным не подавать оба правила вместе, а сначала, на первом уроке, сформулировать правило умножения двух чисел с одинаковыми знаками и отработать умение применять это правило, а потом уже на следующем уроке аналогичным способом сформулировать и закрепить правило умножения двух чисел с разными знаками.
Задача 1. Температура воздуха в этот час повышается на 2 °С. Сейчас термометр показывает 0 °С. Какую температуру воздуха будет показывать термометр через три часа?
Решения. Поскольку температура каждый час повышается на 0 °С, то через три часа она будет: +2 + (+2) + (+2) = 2 · (+3) = +6.
Имеем: +2 · (+3) = +6. (1)
Задача 2. Температура воздуха понижается каждый час на 2 °С. Сейчас термометр показывает 0 °С. Какую температуру показывал термометр три часа назад?
Решения. Очевидно, что поскольку температура ежечасно снижалась на 2 °С, а сейчас 0 °С, то три часа назад она была 6 °С.
Поскольку температура снижалась, то ежечасное изменение температуры сказывается -2 °С, время, что прошло, - 3 ч. Тогда, чтобы получить ответ, достаточно (-2) · (-3) = +6. (2)
Если рассмотреть другие подобные задачи и записать равенства, аналогичные (1) и (2), а затем сравнить их, и можно прийти к выводу:
Чтобы умножить два числа с одинаковыми знаками, надо перемножить модули этих чисел (и перед результатом поставить знак «+») или
Произведением двух чисел с одинаковыми знаками есть число, равное произведению модулей этих чисел.
Например
а) (+5) · (+7) = |+5| · |+7| = 35;
б) (-4) · (-0) = |-4| · |-8| = 32.
@ Чтобы предупредить возможные ошибки, обращаем внимание учащихся на то, что в правиле речь идет о умножения двух множителей. Случай, когда множителей больше, требует отдельного рассмотрения. Если у учеников возникнет такой вопрос, надо сообщить, что это будет рассматриваться позже.
VI. Закрепления знаний. Выработка умений
Устные упражнения
1. Прочитайте выражения: +2,4 · (+0,5); -2,4 · (-0,5).
2. Выполните умножение:
а) +7 · (+8); б) (-6) · (-9); в) (-10) · (-18); г) 0,4 · (+0,6); д) (-0,5) · (-0,8); е) 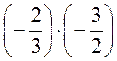 ; ж) (-0,01) · (+10); с) (-0,001) · (-100).
; ж) (-0,01) · (+10); с) (-0,001) · (-100).
Письменные упражнения
1. Найдите произведение:
а) 0,3 · (+0,9); б) -3,2 · (-20,1); в) -10 · (-3,2); г) (+0,16) · (+3); д) -2,4 · (-1,5) есть) -2,49 · (-7,08); ж) 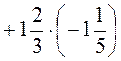 ; з)
; з) 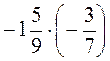 ; к)
; к) 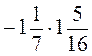 ; л)
; л) 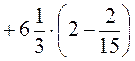 .
.
2. Выполните действия:
а) -14,3 · (-0,6) - (-5,7) · (-1,4);
б) (23,42 - 54) · (-4,12 + 4,04);
в) 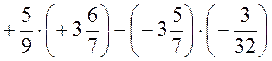 ;
;
г) (-18 + 5,2 - 9,7) · (-3,4 - 8,9 + 12,2);
д) 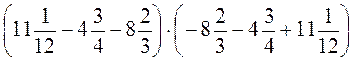 ;
;
есть) -3,2 · (-14,7+ (-0,9) - (14,7));
же) -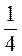 ·(0,315 - (-0,684) - 1,799).
·(0,315 - (-0,684) - 1,799).
Упражнения на повторение
1. Представьте выражение в виде алгебраической суммы и вычислите его значение:
а) -20 - (-12); б) 75 - (-48); в) -14 - (+38); г) 24 - (+42);
д) -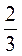 + (-1) -
+ (-1) - 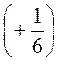 +(-5,2); ) 40 - (-3,7) - (+6,2) +
+(-5,2); ) 40 - (-3,7) - (+6,2) + 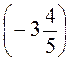 ; ) -18 - (-42,5) + (-15,7) -
; ) -18 - (-42,5) + (-15,7) - 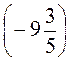 ; с) -40 +
; с) -40 + 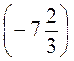 +
+ 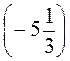 - (-9,3).
- (-9,3).
2. Найдите такие отрицательные значения х и у, чтобы значение выражения х - у равно: а) -10; б) 2,5; в) 0; г) 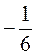 ; д) 1; е) 0,1.
; д) 1; е) 0,1.
3. Альбом дороже книги на 1,2 грн. Сколько стоит книга и сколько альбом, если известно, что:
а) альбом дороже книги в 1,5 раз;
б) книга в 1,6 раза дешевле альбома;
в) стоимость книги составляет 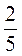 цены альбома;
цены альбома;
г) цена книги составляет 80 % от цены альбома?
V. Итог урока
Вопрос к классу
1. Как умножить два рациональных числа с одинаковыми знаками?
2. Что больше: произведение +2 и +5 или произведение -3 и (-4)?
VI. Домашнее задание
Устные упражнения
1. Какой знак имеет произведение: а) - 5 · (-1,2); б) 7 · (-89)?
2. Вычислите: -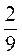 · (-3).
· (-3).
3. Какой знак имеет произведение ab, если:
а) а > 0, b > 0;
б) a > 0, b 0;
в) а 0, b 0;
г) a 0, b > 0;
д) а 0, b = 0;
е) a = 0, b > 0?
Письменные упражнения
1. Выполните умножение: а) -10 · (-70,1); б) -5,45 · (-1,02); в) 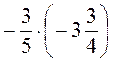 .
.
2. Вычислите: а) - 0,4 · (- 10) - 7; б) 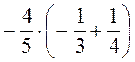 .
.
3. Поставьте вместо звездочки знак «» или «>» так, чтобы образовалась правильная неравенство: - 7,2 · (- 15) * (100).
Упражнение на повторение
Сумма двух чисел равна 12,5, причем одно число в 4 раза больше второго. Найдите эти числа.