Часть 3 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Раздел 8 ЭЛЕКТРИЧЕСТВО

8.5. Вектор электрической индукции. Теорема Остроградского-Гаусса

Предположим, что точечный заряд q находится в центре сферического воздушного пузырька, который находится в определенной среде, например в масле, диэлектрическая проницаемость которого ε=2. Напряженность электрического поля вблизи границы раздела воздух - масло на расстоянии r от заряда, меньшей радиуса пузырька,

Достаточно лишь перейти грань разделения, как напряженность поля в точке, которая размещается в масле бесконечно близко к границе разделения, станет меньше в е раз (ε = 2):

Следовательно, напряженность на границе раздела двух сред скачкообразно изменяется. Поэтому изображение электрического поля помощью силовых линий усложняется. Если среда, в которой реализуется электростатическое поле, неоднородное, то есть характеризуется различными значениями диэлектрической проницаемости, то для характеристики поля удобнее использовать другую величину, которая, в отличие от напряженности, не изменяется скачкообразно вблизи поверхности раздела двух различных диэлектриков. Эту величину называют вектором электрической индукции 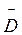. Она связана с вектором напряженности таким соотношением:

Из приведенного равенства следует, что индукция при переходе через границу раздела двух диэлектриков остается неизменной, поскольку изменение 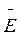при переходе в среду с диэлектрической проницаемостью ε компенсируется соответствующим множителем.

Поскольку для вакуума и практически для воздуха ε = 1, то для них 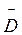= ε₀.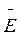

Если электрическое поле создано одним точечным зарядом q, то вектор электрической индукции на расстоянии r от заряда будет

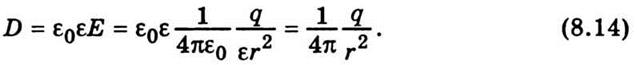
По аналогии с силовыми линиями (линиями напряженности) для графического изображения электростатических полей используют линии электрической индукции. Количество линий индукции, что проходят через произвольную поверхность, проведенную в поле, называют потоком вектора электрической индукции через эту поверхность.

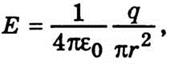Вычислим поток вектора электрической индукции через поверхность сферы радиуса r, в центре которой находится заряд q, создающий электрическое поле. Поскольку напряженность электрического поля в каждой точке сферической поверхности то через единицу поверхности проходит линий напряженности Е или D линий индукции. Тогда поток вектора электрической индукции, пронизывающего поверхность сферы радиуса r, можно определить так:

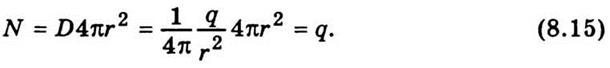
Нетрудно доказать, что полученный результат справедлив не только для случая сферической поверхности, но и для любой замкнутой поверхности, внутри которой в произвольной точке содержится точечный заряд q.

Формулу (8.15) можно обобщить и на случай, когда поле создано системой точечных зарядов q₁, q₂,..., q_n. Учитывая принцип суперпозиции электрических полей, достанем

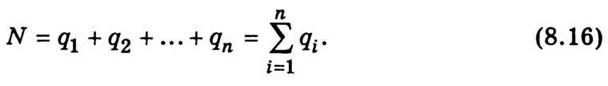
Следовательно, поток вектора электрической индукции через произвольную замкнутую поверхность не зависит от диэлектрических свойств среды и равен алгебраической сумме электрических зарядов, содержащиеся внутри этой поверхности. Полученный результат называют теоремой Остроградского - Гаусса.

Теорему Остроградского - Гаусса применяют для расчета индукции (или напряженности) полей, которые создаются произвольным зарядом, поскольку любой заряд можно представить в виде суммы бесконечно большого количества точечных зарядов.