Урок № 78

Тема. Рациональные числа; сравнение, сложение и вычитание. Решение упражнений

Цель: подготовить учащихся к выполнению тематической контрольной работы.

Тип урока: обобщение и систематизация знаний, умений и навыков.

Ход урока

I. Проверка домашнего задания

@ Если на предыдущем уроке не успели сделать, то в начале этого урока мы проводим тестовую работу (из темы «Раскрытие скобок») (см. урок № 80). Чтобы иметь возможность проанализировать правильность выполнения работы, ученики, выполнив действия в тетрадях и выбрав правильный, на их взгляд, вариант ответа, записывают его обозначения как в тетрадях, так и на листе ответов (который, после того как будут собраны ответы, остается в учеников).

II. Обобщение и систематизация знаний

Устные упражнения

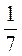1. Прочитайте числа: 4,2; -3; -8; 1000; 0; - 2,87; 3. Которые из них являются: а) отрицательными; б) положительными; в) неотъемлемыми; г) недодатними.

2. Назовите координаты точек А, В, С, D, изображенных на рисунке.

Какие точки имеют целые координаты? натуральные координаты? дробные координаты?

3. Назовите числа, противоположные числам: 7; - 4; 0; -4,5; 3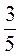; 15,6; -3. Чему равны модули образованных чисел?

4. Игровой момент «самый Умный»

Тестовые вопросы

На доске записано, например, дробное отрицательное число -3.

Ученик должен быстро ответить на вопросы, которые учитель задает в краткой форме:

1) Какое число?

2) Его модуль.

3) Где расположен координатной прямой?

4) Между какими соседними целыми числами?

5) Два числа, меньшие от него.

6) Два числа (недодатних), больших за него.

7) Обратное к нему число.

8) Расстояние в единичных отрезках между этим числом и ему противоположным на координатной прямой.

@ Во время выполнения устных упражнений учащиеся повторяют основные понятия и алгоритмы первого блока темы «Координатная прямая и сравнение рациональных чисел».

III. Совершенствование умений

1. Начертите координатную прямую с единичным отрезком 1 см (2 клетки). Отметьте на этой прямой:

а) точки А(3); В(-4,5); С(-2); D(-3); Е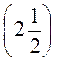; F(4,5);

б) точку М 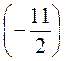и точку К, что имеет противоположную координату;

в) точки, модули координат которых равны 3,5; 4; 0.

2. Даны числа: 5; 3,7; -2; -309; 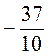; 2,5; 3,125; 0; -5001; -3.

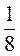а) Какие из данных чисел являются натуральными, целыми, дробными, положительными, отрицательными?

б) Найдите модули чисел; есть среди них такие, что имеют равные модули? Почему?

в) Расположите числа в порядке возрастания.

3. Найдите -b, если b= 1; ; -3,5.

4. Вычислите:

а) |-1,5| + |0,98|; б) |-1100| - |-295|; в) |-2,4| · 2,5 - 6; г) |-27| : |-180| + 0,4; д) 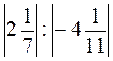; е) 1,6 + 1 - .

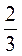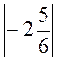5. На координатной прямой отметьте точки, которые удовлетворяют неравенство: а) |х| 5; б) 4 > |x|.

Запишите все целые числа, которые удовлетворяют каждую неровность.

IV. Итоги урока

Тестовые задания

1. Какая из перечисленных точек является на представленном рисунке началом отсчета: 1) А; 2) В; 3) С; 4) D.

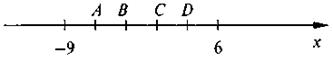
2. Какие из представленных чисел размещены на координатной прямой вправо от числа -1, 3?

1) -1,4; 2) -1,15; 3) -2; 4) -1,31.

3. Какое из приведенных утверждений правильное?

1) Числа 5 и -5 - натуральные числа;

2) числа 5, 6, 4 и -7 - целые числа;

3) из четырех чисел: - 2; 6; 9; 8 2 - целое число;

4) на координатной прямой между числами -3 и 2 содержатся 4 целых числа.

4. Вычислите значение выражения |х| + |у|, если х = -3, у = -5.
1) 8; 2) -8; 3) -2; 4) 2.

V. Домашнее задание

1. Даны числа: 5; - 8; 4,25; 1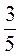; 506; 8; -1,6; 0,125; -206; -4.

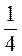а) Какие из данных чисел являются натуральными; целыми; дробными?

б) Запишите числа, противоположные данным.

в) Найдите модули чисел. Есть среди них такие, что имеют равные модули?

г) Расположите данные числа в порядке возрастания.

2. Начертите координатную прямую с единичным отрезком 1 см. Отметьте на координатной прямой:

а) точки А(-2), В(-3,5), С(-0,5), D(2,5), Е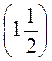, F(4);

б) точку K(-1,5) и точку, что масс противоположную координату;

в) точки, модули координат которых равны 2; 3,5; 0.

3. Укажите одно число, которое:

а) больше , но меньше ;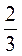

б) меньше -, но больше от -;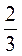

в) меньше - 3,3, но больше - 3,4.

4. Найдите: а) |-y|, если в = 2,3; -0,6; б)|-(-с)|, если с = -2; 1.