|
II. Актуализация опорных знаний Устные упражнения
2. Среди выражений найдите уровне: a) a + (b + c); б) а - (b + с); в) (а + b) - с; г) a - b - c; д) а + b - с; е) a - c + b; ж) а + b + с; с) а + с - b; к) а; л) +а; г) -(-а). 3. Прочитайте записи, используя слова «число, противоположное...»: а) -(-5); б) -3,2; в) Как упростить эти записи? 4. Замените вычитание добавлением в выражениях: а) 4 - 6; б) 4 - (-6); в) а - b; г) а - (b + с); д) а - (-b + с). 5. Вычислите удобным способом: -3 + (3 + (-5)); -12 + (-14 + 28).
III. Формирование знаний @ Эта тема является очень важной для успешного изучения математики в последующих классах. Поэтому надо, уже начиная с этого урока, требовать от учащихся понимания и точного усвоения и воспроизведения правил раскрытия скобок; не менее важным является и отработка навыков применения этих правил для упрощения выражений. Для лучшего понимания (а следовательно, и запоминания) правил предлагаем немного отступить от текста изложения материала, который традиционно представлены в учебниках, а именно: сначала опять же на конкретных примерах показать выполнение этих правил (не забывайте - шестиклассники пока что в основном имеют конкретное, а не развито логическое мышление), а потом уже формулировать соответствующие общие правила. Мотивация учебной деятельности Упражнения № 2-5 (см. устные упражнения) нам показывают, что, во-первых, есть такие свойства, которые помогают изменять порядок выполнения действий в выражениях, а также, во-вторых, заменять одни действия другими. Сегодня на уроке мы узнаем о еще один способ «превращения» выражений, а именно: «раскрытие скобок». Раскрытие скобок, перед которыми стоит знак «+» Задача 1. Вычислите значения выражений и сравните результаты. а) 11 + (45 - 17); б) (11 + 45) + (-17); в) 11 + 45 - 17; г) 11+ (-17 + 45); д) 11-17 + 45; есть) (11 + (-17)) + 45. Решения. Понятно, что после выполнения действий во всех выражениях получим одинаковое значение выражений, а именно: 39. Сравнив сами выражения, видим, что они отличаются только наличием или отсутствием скобок, поэтому можно записать 11 + (45 - 17) = 11 + 45 - 17, видим, что этот результат можно было получить, раскрыв скобки, а потому делаем вывод 1. Чтобы раскрыть скобки, перед которыми стоит знак «+», надо: 1) опустить скобки и знак «+», что стоят перед ними; 2) записать все слагаемые со своими знаками: a + (b + c) = a+b+c. Например,
Задание 2. Вычислите значения выражений и сравните результат: а) -6 + 4; б) -(-6 + 4); в) 6 + (-4). Решения. Очевидно, что имеем в п. а) -2, а в п. б), в) 2. Можем записать это так: -(-6 + 4) = 6 + (-4) - это число, противоположное значение выражения (-6 i 4). Сравнив записи, заметим, что выражение, противоположный суммы, является также сумма, но слагаемые являются противоположными данных. Вывод 2. Выражение, противоположный суммы, есть сумма противоположных слагаемых. Например а) -(3 - 4) = -(3 + (-4)) = -3 + 4 = 1; б) -(a + b)= -a + (-b) = -a - b; в) -(a - b + c) = -a + (b) + (-c) = -a + b - c. Правило раскрытия скобок, перед которыми стоит знак «-» Задача 3. Используя правило вычитания, раскройте скобки в выражении-5 - (3 + 7). Решения. 5 - (3 + 7) = 5 + ( - (3 + 7)) = 5 + (- 3 - 7) = 5 - 3 - 7 = -5 или, заменив числа на буквы, имеем: a - (b + c) = a + (- (b + c)) = a + (-b - c) = a - b - c. Сравнив записи, которые мы имели с дужками, и записи, которые не содержат скобок, приходим к выводу, что скобки, перед которыми стоит знак «минус», раскрываются так. Вывод 3. Чтобы раскрыть скобки, перед которыми стоит знак «минус», надо: 1) опустить скобки и знак «-», стоящий перед ними; 2) все слагаемые, стоящие в скобках, записать с противоположными знаками. Например
III. Закрепления знаний. Усвоение умений Устные упражнения 1. Правильно ли раскрыты скобки? а) 3 + (-5 - 2) = 3 - 5 - 2; б) 3 - (-5 + 2) = 3 + 5 - 2; в) 3 - (5 - 2) = 3 - 5 - 2; г) 3 - (5 + 2) = 3 - 5 + 2. 2. Заполните пропуски ... соответствующими знаками («+» или «-»), чтобы раскрытие скобок было выполнено правильно: а) -3 - (m + n) = ... 3 ... m ... n; б) 5 + (-a + b - c) = ... 5 ... a... b. . с; в) 7 - (-k + г + t) = ... 7... k ... p ... t; г) m + 3 - (m - n + 4) = ... m ... 3 ... m ... n ... 4; д) m + 3 - (m - n) + 4 = ... m ... 3 ... m ... n ... 4. @ Типичная ошибка учащихся во время раскрытия скобок, перед которыми стоит знак «-»: меняют знак всех слагаемых - и тех, что стоят в скобках, и тех, что стояли вне скобок. Поэтому, чтобы предупредить эти ошибки, сразу обращаем внимание на тот момент, что во время раскрытия скобок меняется знак только в тех слагаемых, стоящих в скобках.
Письменные упражнения I уровень 1. Вычислите: а) - 6 + 9 + 6; б) - 7 + 9 + (- 2); в) - 5 + 31 + 5 + (- 31); г) - 27 + 5 + (- 4) + 27; д) - 7 + 11 + 8 - 12; есть) 3 + 7 + (- 3) + (- 1). 2. Раскройте скобки: а) 5 + (m - n); б) 7 - (-а + b); в) -3 - (m + n); г) 5 - (а - b + с). 3. Раскройте скобки и упростите выражение: а) 0,9 - (а + 3,7); б) - (4 - а + 0,2) - 11,8; в) b + (7,8 - b - 1,9), г) - (а + 5,1) - (-а - 4,9).
II уровень (если успеем) 4. Упростите выражение a + b - (b - c) + d и найдите его значение, если a = -3,1; b = 0,017, с = -0,2; d = -5.
V. Итог урока Вопрос к классу 1. Как раскрыть скобки, перед которыми стоит знак «+»? 2. Как раскрыть скобки, перед которыми стоит знак «-»?
VI. Домашнее задание 1. Раскройте скобки и найдите значение выражения: а) - 32 - (53 - 72); б) 40 - (- 17 + 35); в) - 12 + (- 32 - 17); г) - 3,8 -(-8,1+ 3,9); д) 7,5 + (- 8,4 + 7); есть) 2. Упростите выражение: а) -0,24 - (5,6 - а); б) 4,1 - (5,2 + b - 1,5); в) - (-5 + а) - 7,2; г) - (а - 6) + (4,2 + а - 5,8). Упражнения на повторение 1. Периметр треугольника ABC равен 15 см. Длина стороны АВ составляет 44 % периметра, а длина стороны ВС составляет 2. Решите уравнение: а) 5 + х = -7,8; б) 4 - х = -1,2.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
-
; е) 2
-
-
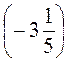
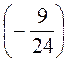; е) 2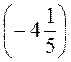
-
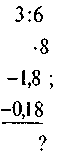
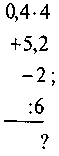
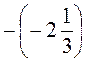; г) -; д) -(а + 1); е) -(-а).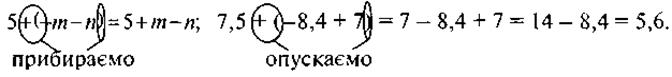
.
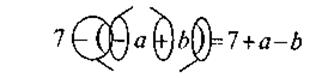
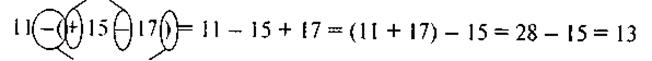
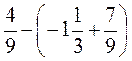