Урок № 75
Тема. Вычитание рациональных чисел. Алгебраическая сумма чисел
Цель: основываясь на знаниях учащихся о правила и свойства сложения и вычитания рациональных чисел, сформировать представление о содержании понятия «алгебраическая сумма» и выработать умения применять полученные знания для вычисления алгебраических сумм.
Тип урока: применение знаний, умений и навыков.
Ход урока
И. Проверка домашнего задания. Актуализация опорных знаний
@ Особое внимание обращаем на задания 1 и 2 (желательно записать решение на доске или учителю, или вызвать нескольких учеников к доске).
Устные упражнения
1. Вычислите:
а) 17 + 0,3; 0,005 + 25; 0,37 + 2,03; 3,84 + 0,2; 1,27 + 2,3;
б) 0,728 - 0,7; 0,8 - 0,25; 1 - 0,6; 0,7 - 0,07; 3 - 0,85;
в) 7 - (+3); +7 - (-3); (-7) - (+3); (-7) - (-3);
г) -0,4 - (0,5); +0,4 - (-0,5); -0,4 - (-0,5); +0,4 - (+0,5).
2. Запишите в виде суммы и упростите: а) -3 - (-а) - 5; б) 2,7 - b - 3; в) 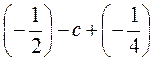 .
.
3. Найдите значение суммы удобным способом:
а) -2 + (-3,5) + 2 + 3 + (-7);
+ (-7);
б) 6,65 + 0,353 + (-0,003);
в) -2 + (-3) + (-5) + 2 + 3 + 5.
4. * Вите Верхоглядкіну учитель предложил дома выполнить такое задание: найти сумму всех целых чисел от -599 к 601. Витя садится за работу, но работа идет медленно. Тогда на помощь приходят мать, отец, сестра и брат. Вычисляли, пока от усталости не стали заплющуватися глаза, и при этом все ругались на учителя, который задает маленьким детям такие задачи.
А как бы вы решили эту задачу? Напомню, что надо найти сумму -599 + (-590) + (-597) + (-546) + ... + 597 + 548 + 599 + 600 + 601.
II. Мотивация учебной деятельности
@ Последнее задание устных упражнений очень хорошо показывает учащимся, что знание свойств действий помогает им значительно упрощать вычисления. Надо также добавить, что знание некоторых моментов позволяет еще и упрощать записи.
II. Дополнение знаний
@ Желательно напомнить, что в математике есть определенные договоренности относительно записей (сокращенных) некоторых выражений (можно напомнить о сокращенную запись произведения числа и буквы а: 2·а = 2а, запись суммы одинаковых слагаемых в виде произведения, запись произведения одинаковых множителей в виде степени с натуральным показателем и др.). Тогда понятна будет попытка сделать более краткая запись суммы рациональных чисел (в виде алгебраической суммы). Важно требовать от учащихся осознания того, что если в записи последовательно записаны числа, между которыми нет скобок и стоят только знаки «+» или «-», то мы имеем сумму, а знаки «+» или «-» являются не знаками действия, а знаками слагаемых, а следовательно, сигнализируют о том, какой порядок вычислений является самым удобным в данном случае.
Понятие алгебраической суммы
Пример 1. Запись(-9) + (+4) + (0) + (-5) + (+2) - сумма 5 слагаемых. Договоримся знаки действия сложения, стоящих между слагаемыми не писать, а записать только числа с их знаками без скобок: -9 + 4 + 0 - 5 + 2 - алгебраическая сумма.
Найдем числовые значения этой суммы:
1) 4 + 2 = 6;
2) -9 - 5 = -14;
3) + 6 + (-14) = -8.
Итак, (-9) + (4) + (0) + (-5) + (+2) = -9 + 4 + 0 -5 + 2 = -8.
Пример 2. Запишем выражение: 10 - (+9) + (-8) - (-6).
Мы видим, что это не сумма. Использовав соответствующее правило замены вычитания, запишем это выражение сначала в виде суммы, а затем в виде алгебраической суммы:
10 - (+9) + (-8) - (-6) = 10 + (-9) + (-8) + 6 = 10 - 9 - 8 + 6 = 1.
1) 10 + 6 = 16;
2) -9 - 8 = -17;
3) 16 + (-17) = -1.
IV. Отработка навыков
Устные упражнения
1. Вычислите алгебраические суммы. Назовите слагаемые в алгебраической сумме: -1 - 2 - 3 - 4; +1 - 2 + 3 - 4; - 1 + 2 - 3 + 4; 1 - 2 - 3 + 4.
2. Вычислите алгебраическую сумму:
а) 5 - 3 + 1 - 4; -5 + 3 - 1 + 4; -5 - 3 + 1 + 4;
б) - 7 + 2 - 5 + 6; 7 - 2 + 5 - 6; -7 + 2 - 5 - 6.
Письменные упражнения
1. Представьте выражение в виде алгебраической суммы и вычислите его:
а) (-13) - (-8);
б) 10 - (+6);
в) -9 - (-11);
г) 16 + (-4) - (+5);
д) -3 - (-7) + (-5);
есть) -12 - (+3) + (-4) - (-6).
2. Вычислите значение алгебраической суммы:
а) 15 - 12 - 13;
б) -16 - 9 + 7;
в) -20 - 3 - 14;
г) -13 - 18 - 6 + 14;
д) -17 + 24 - 8;
есть) 4 - 15 + 9;
ж) - 19 - 7 + 12;
с) -18 + 7 - 5 + 9.
3. Выполните действия:
а) - 3 - (+2,7) + 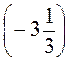 -
- 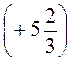 ;
;
б) 0 - 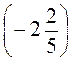 +
+ 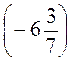 -
- 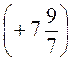 -
-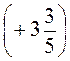 ;
;
в) (-25,6) + (-21,4) + (+3,1) + (+ 8,4);
г) (-16,2) + (-37,3) + (+5,1) + (-11,3).
4. Составьте сумму из следующих слагаемых и запишите ее в виде алгебраической суммы и упростите (если можно).
а) -х; -у; -4,8; б) 1,5; -а; b; с; в) г; -20; 6; -k; 10,3; г) 7,6; m; -n; -t; -l.
5. Между какими соседними целыми числами расположено число: - 21; 2;  ; -
; -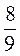 ;
; 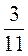 ; -7,2; -
; -7,2; -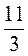 ?
?
6. Найдите число, противоположное -7,2; 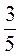 ; -2
; -2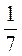 ; 3,85.
; 3,85.
7. Решите уравнение: а) - х = 3,5; б) - х = - 7,2 + 9; в) - m = -6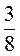 +
+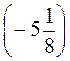 .
.
V. Итоги урока
Среди следующих записей найдите алгебраическую сумму и вычислите ее значение:
а) -3 + (-5) + (+2) - (+4); б) -3 - 5 - (-2) - (-4);
в) - 3 - 5 + 2 + 4; г) - (-3) -5 + 2 + 4.
VI. Домашнее задание
1. Найдите значение выражения:
а) 24 - (-13) - (-12);
б) -33 - 16 - (-11);
в) -4,3 - 5,4 - 2,6;
г) 4,7 - (-2) - (-1,5);
д) 1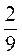 - 1
- 1 + 1
+ 1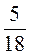 ;
;
е) -7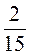 + 4
+ 4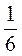 - 1,2.
- 1,2.
2. Решите уравнение:
а) -p = - 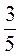 ; б) -k = 11 + (-12,3); в) -в = -13 +
; б) -k = 11 + (-12,3); в) -в = -13 + 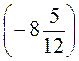 .
.
3. Задача. В трех ящиках 21 кг гвоздей. В первом ящике в 1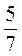 раза больше гвоздей, чем во втором. Масса гвоздей третьего ящика составляет
раза больше гвоздей, чем во втором. Масса гвоздей третьего ящика составляет 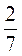 массы гвоздей второго ящика. Сколько килограммов гвоздей в каждом ящике?
массы гвоздей второго ящика. Сколько килограммов гвоздей в каждом ящике?
4. Отметьте на координатной прямой точки А(-4) и B(9). Найдите расстояние между точками А и В в единичных отрезках.