Урок 75
Тема. Смешанные числа
Цель: дополнить
знания учащихся об алгоритмах действий сложения и вычитания смешанных чисел; сформировать
умение выполнять сложение и вычитание смешанных чисел и решать задачи,
в которых предусмотрено использование этих действий.
Тип урока:
усвоение новых знаний.
Ход урока
I. Проверка
домашнего задания
Математический
диктант
Вариант 1 [2]
1. Запишите неправильный дробь в виде
смешанного числа 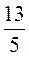
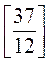 .
.
2. Запишите долю в виде дроби и выделите
из полученной дроби целую и дробную часть от деления 25 : 8 [7 : 2].
3. Запишите число в виде неправильной
дроби 9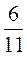
 .
.
4. Запишите число 3 [5] в виде дроби с
знаменателем 7 [4].
5. Какое наибольшее натуральное число удовлетворяет
неравенство 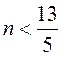
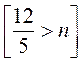 ?
?
II. Актуализация
опорных знаний
1. Вычислите, используя свойства
добавление:
1) 23 + 45 +
77;
2) (217 + 528) +
(12 + 113).
2. Как в виде дроби со знаменателем 3
записывают число:
1) 5; 2) 10; 3) 17;
4) 120?
3. Заполните цепочку вычислений:
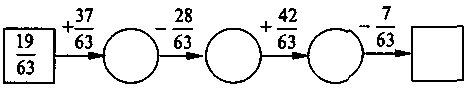
4. Сравните значения
выражений:
1)  и
и 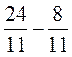 ; 2)
; 2) 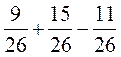 и
и 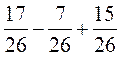 .
.
III. Усвоение знаний
1. На прилавке лежит
3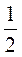 головки сыра и рядом 2 такие же. Сколько
сыра на прилавке?
головки сыра и рядом 2 такие же. Сколько
сыра на прилавке?
Решения. Понятно, что надо добавить 3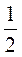 и 2 (рис. 119)
и 2 (рис. 119)
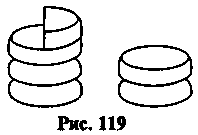
Найдем количество
целых головок сыра: 3 + 2 = 5. Затем к этому числу добавим 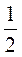 головки: 5 +
головки: 5 + 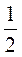 = 5
= 5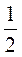 . Итак, 3
. Итак, 3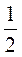 + 2 = 5
+ 2 = 5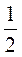 .
.
2.
На
прилавке лежит 3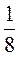 головки сыра и рядом еще 2
головки сыра и рядом еще 2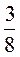 головки. Сколько сыра лежит на прилавке?
(Рис. 120).
головки. Сколько сыра лежит на прилавке?
(Рис. 120).
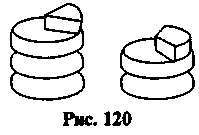
Решения. Для
решение задачи добавим 3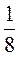 к 2
к 2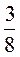 . Сначала найдем количество целых
головок: 3 + 2 = 5.
. Сначала найдем количество целых
головок: 3 + 2 = 5.
Потом добавим 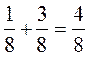 , составив
, составив 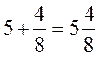 . Следовательно,
. Следовательно, 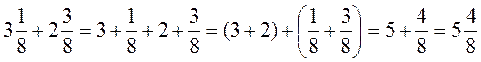 .
.
То есть, чтобы добавить
два смешанных числа, надо отдельно добавить их целые и дробные части.
На закрепление желательно
рассмотреть примеры.
3.
Выполните
добавление:
1) 8 + 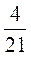 ;
;
2) 5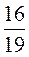 + 3
+ 3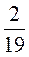 ;
;
3) 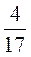 +
+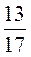 ;
;
4) 5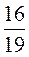 +3
+3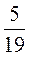 ;
;
5) 5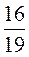 + 3
+ 3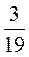 .
.
(В примере 4)
подайте развернутый запись преобразований: 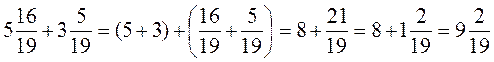 , потому
, потому 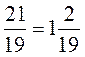 . )
. )
4. Проверьте
добавлением правильность выполнения вычитания:
1) 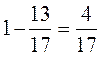 ;
;
5. 2) 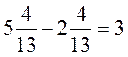 ;
;
6. 3) 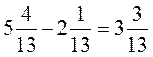 ;
;
7. 4) 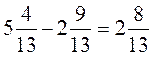 .
.
Решения. 1) 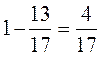 правильно, потому что
правильно, потому что 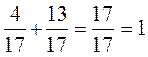 ;
;
2) 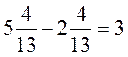 правильно, потому что
правильно, потому что 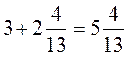 ;
;
3) 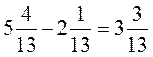 правильно, потому что
правильно, потому что 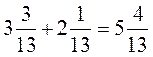 ;
;
4) 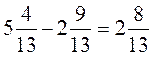 правильно, потому
правильно, потому 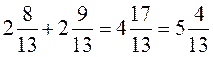 .
.
Следовательно, можно
отметить, что:
1) если дробная часть уменьшаемого больше от дробной
части вычитателя или равна ей, то, чтобы отнять два смешанных числа, надо
от целой и дробной части уменьшаемого вычесть соответственно целую и дробную
части вычитателя;
2) в других случаях - от целой части уменьшаемого
«одалживаем» 1 и подаем ее в виде неправильной дроби со знаменателем,
равна знаменателе дробной части.
IV. Закрепление знаний
и формирования умений
Решение упражнений
№№ 748; 750 (1;3; 5; 7; 9; 11; 13); 752 (1,2). Дополнительная задача №
4.
Методические
рекомендации
@ Сложение смешанных чисел вообще не
вызывает у учащихся затруднений, кроме случая, когда в сумме появляется неправильный
дробь (особенно, когда ученики пытаются добавлять устно). Поэтому надо настоять на
письменном решении задач и каждый раз проверять, не записана сумма
в виде а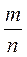 , где
, где 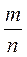 - неправильный
дробь.
- неправильный
дробь.
Относительно вычитания
смешанных чисел, то учитель должен требовать от учеников предварительного анализа условия
примеров, задавая вопросы такого, например, содержания:
1. Есть дробная часть в уменьшающемся и
від'ємнику?
2. Если да, то дробная часть
уменьшаемого равна дробной части вычитателя или больше от нее? Если
так, то вычитаем по правилу. Если нет, то 1 или 2.
3. «Одалживаем» у целой части уменьшаемого 1
и подаем ее в виде 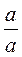 , где а - знаменатель
дробной части вычитателя.
, где а - знаменатель
дробной части вычитателя.
Дополнительная задача.
Из чисел 2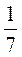 ; 8
; 8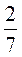 ; 1
; 1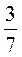 ; 5
; 5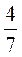 ; 3
; 3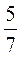 ; 4
; 4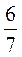 выберите такие, чтобы
их сумма была натуральным числом. Будет ли сумма всех шести слагаемых натуральным
числом?
выберите такие, чтобы
их сумма была натуральным числом. Будет ли сумма всех шести слагаемых натуральным
числом?
V. Домашнее задание
п. 26, № 749; № 751
(1, 2, 3,4, 6); 752 (3); повторить 767.