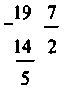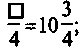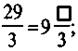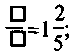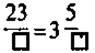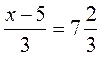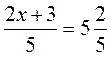Урок 74
Тема. Смешанные числа
Цель: сформировать
понятие «смешанное число, целая и дробная часть числа»; формирование алгоритмов
выделение целой части из неправильной дроби и записи смешанного числа в виде
неправильной дроби; научить учащихся применять названные алгоритмы во время
решения упражнений.
Тип урока:
усвоение новых знаний.
Ход урока
И. Проверка
домашнего задания и актуализация опорных знаний
Устные упражнения
1. Из следующих выражений равна дробь 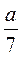 ?
?
1) а + 7; 2) а - 7;
3) а - 7; 4) а : 7.
2. Ответом к какой из следующих задач является
число 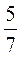 ?
?
1) Зайдите долю
чисел 7 и 5.
2) Сколько
шоколадок получил каждый из 7 учеников, если между ними поровну поделили 5 шоколадок?
3) С какой скоростью
шел пешеход, если за 7 часов он прошел 5 км?
4) Из 7 м ткани
сшили 5 платьиц. Сколько метров ткани пошло на каждое платье?
5) Решите
уравнение 6х = 5.
3. Решите уравнение:
1) 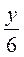 = 3; 2)
= 3; 2) 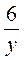 = 3; 3) 3в = 6; 4) 6y = 3.
= 3; 3) 3в = 6; 4) 6y = 3.
4.
Вычислите:
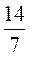 +
+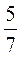 ;
; 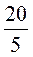 +
+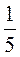 ;
; 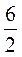 +
+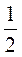 ;
; 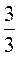 +
+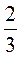 ;
; 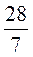 +
+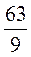 .
.
II. Формирование знаний
@ Материал урока
(понятие смешанного числа и алгоритмы представление неправильной дроби в виде
смешанного числа и наоборот) учитель излагает близко к тексту учебника по
плану:
1. Примеры, приводящие к понятию смешанного
числа.
2. Понятие смешанного числа.
3. Неправильные дроби можно представить в
виде смешанного числа?
4. Алгоритм представления неправильной дроби в
виде смешанного числа. Пример.
5. Алгоритм представления смешанного числа в виде
неправильной дроби. Примеры.
Следует также иметь в
виду, что ученики очень часто путают, какой компонент деления числителя остачею
на знаменатель писать в целую часть, который в числитель, а в знаменатель. Поэтому
на первых уроках можно предложить ученикам такую разноцветную схему (рис.
118):
Рис. 118
III. Закрепление материала. Формирование умений учащихся
Решение упражнений
№№ 742; 744; 746; 759; 761; дополнительные задачи №№ 1-6.
@ Поскольку алгоритмы преобразований
неправильной дроби в смешанное число и обращен к нему являются достаточно сложными для
запоминания, не следует требовать от учащихся воспроизводить их (эти фрагменты
текста п. 26, выделены жирным курсивом). Надо добиться от учащихся понимания
алгоритмов и умений применять их, а для этого лучше всего - решить как можно
больше соответствующих примеров.
Дополнительные задачи
1. За неделю семья потребила 8 кг картофеля.
Сколько килограммов картофеля израсходовали за 1 день?
2. Турист прошел 25 км за 4 ч. Найдите
скорость туриста. Какое расстояние он пройдет за 2 ч.?
3. Ученик решил 12 уравнений за 40 мин.
Сколько минут он решал каждое уравнение? Сколько секунд он потратил на
решение каждого уравнения?
4. У Винни-Пуха несколько банок, вмещающих 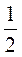 кг меда. Сколько понадобится таких
банок, чтобы разложить в них 6
кг меда. Сколько понадобится таких
банок, чтобы разложить в них 6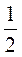 кг меда?
кг меда?
5. Вместо квадратиков запишите такие числа,
чтобы образовались правильные равенства:
1) 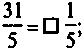 2)
2)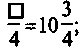 3)
3)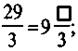 4)
4)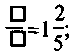 5)
5)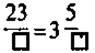
6.
Решите
уравнение:
1) 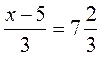 ; 2)
; 2) 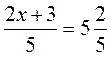 ; 3)
; 3) 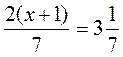 .
.
IV. Итог урока
Вопрос к классу
1. Приведите пример неправильной дроби, который:
1) можно представить в виде смешанного числа; 2) можно представить в виде
натурального числа.
2. Правильная ли равенство?
1) 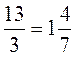 ; 2)
; 2) 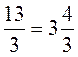 ; 3)
; 3) 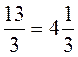 .
.
V. Домашнее задание
п. 26, №№ 743; 745
(1, 3, 5); 747; 760; 762.