УРОК 73

Тема. Дроби и деление натуральных чисел

Цель: показать связь между действием деления и обыкновенными дробями; выработать навыки записи доли в виде дроби из натурального числа и дроби с произвольным наперед заданным знаменателем.

Тип урока: усвоение новых знаний.

Ход урока

И. Актуализация опорных знаний

Вопрос к классу

1. Пирог разрезали на 8 равных кусков.

1) Какую часть пирога составляет 1 кусок?

2) Какую часть пирога составляют 3 куска?

3) Какую часть пирога составляют все куски?

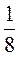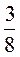[1); 2) ; 3) .]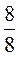

Итак, если целое разделить на b равных частей и взять а таких частей, получим дробь .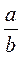

II. Усвоение новых знаний

Учитель предлагает учащимся решить задачи.

1. Разделить поровну 6 плиток шоколада между тремя детьми.
Решения. Понятно, что 6 делится на 3 наділо, поэтому 6 : 3 = 2 (куски) каждом.

2. Разделить поровну 3 плитки шоколада между тремя детьми.
Решения. Понятно, что 3 делится наділо на 3, поэтому 3 : 3 = 1 (кусок) каждом.

3. Разделить поровну 2 плитки шоколада между тремя детьми (рис. 116).

Решения. Так как 2 не делится наділо на 3, делим каждую плитку шоколада на 3 равных части и дадим каждому с детей по одной части от каждой плитки.

Каждая часть - это 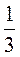плитки, а 2 таких части - это 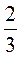плитки. Следовательно, разделив на 2 плитки 3, получили .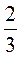

4. Разделить поровну 5 плиток шоколада между тремя детьми (рис. 117).

Решения. Поскольку 5 не делится на 3, каждую плитку шоколада делим на 3 равных части и дадим каждому из детей по одной части от каждой плитки.

Каждая часть - это 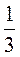, а 5 таких частей 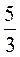. Следовательно, разделив 5 плиток на 3, получили .

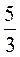Таким образом, можно сказать, что: 2 : 3 = 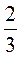; 5 : 3 = .

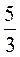И вообще, а : b = 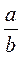, где а и b - любые натуральные числа, если и не равен 0, то есть черту дроби можно заменить на знак деления.

Задание 1 (на закрепление). Записать в виде дроби долю:

1) 2 : 5; 2) 1 : 10; 3) 15 : 8; 4) 7 : 1; 5) 7 : 7; 6) 12 : 4; 7) 15 : 5.

@ Рассмотрев с учащимися примеры 4) 5) 6) 7), учитель должен обратить внимание учащихся, что в каждом из них деления выполняется наділо, то есть дробь равна натуральному числу:

4) 7 : 1 = 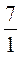= 7; 5) 7 : 7 = 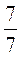= 1; 6) 12 : 4 = 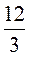= 3; 7) 15 : 5 = 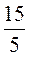= 3.

То есть, «прочитав» эти равенства справа налево, имеем, что натуральное число можно записать дробью, причем (см. примеры 6, 7) - не одним.

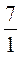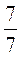7 = ; 1 = ; 3 = 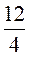= 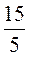и т. д.

Задание 2. Заполнить пустые места в таблице.

После закрепления связи между делением и обыкновенными дробями, ученики по учебнику знакомятся с применением этого правила для решения уравнений (п. 25, пример на с. 181) и, записав пример в тетрадь, начинают решать задачи самостоятельно.

III. Закрепления знаний. Формирование умений

Решение упражнений

№ 735; 737; 740, дополнительные задачи 1, 2, 3, 4.

Задача 1. Выполните деление с остачею:

1) 2738 на 125; 2) 3049 на 134.

Задание 2. На сколько равных частей надо разрезать пирог, чтобы ты мог раздать его поровну своим друзьям, если тебе заранее неизвестно, сколько их будет - три или четверо?

Задача 3. Сад площадью 420 м² засажено яблонями, сливами и вишнями, причем засажено яблонями 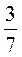площади сада, а сливами - 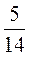площади.

Какая площадь сада засажена вишнями?

Задача 4. Решите уравнение: 7х = 13; 5х + х = 5.

IV. Итог урока

Выполните деление:

1) 14 : 2; 2) 14 : 14; 3) 14 : 3; 4) 14 : 15; 5) 14 : а, а ≠ 0, равна 0;

6) а : 14; 7) m : n, n не равно 0.

Итак, теперь мы знаем, что можно поделить любое натуральное число на другое (кроме 0), причем в отдельных случаях получим натуральное число, а в других - есть дробь.

V. Домашнее задание

п. 25, №№ 734; 736; 738; 739.