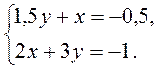Урок № 73
Тема. Системы двух линейных уравнений с двумя переменными и графический способ решения систем
Цель: усвоить знания о зависимости количества решений системы линейных уравнений от соотношения коэффициентов a, b, c этих уравнений; выработка умений применять названную признак во время графического решения систем уравнений; дальнейшее совершенствовать умение решать системы линейных уравнений графическим способом.
Тип урока: усвоение новых знаний.
Ход урока
I. Организационный момент
1. Проверка готовности к уроку.
2. План работы (место урока в теме).
II. Проверка домашнего задания
@ Проверить на уроке желательно не только решение письменных упражнений, но и теоретическую часть. Поэтому в начале урока предлагаем учащимся контрольные вопросы (см. предыдущий урок), а затем проводим интерактивное упражнение «Микрофон». После проверки теоретических знаний, организуем проверку решения письменных упражнений или:
1) как комментарий готового решения (с последующей само - или взаимопроверкой);
2) как игровой момент «Найди ошибку».
III. Формулировка цели и задач урока
@ После проверки домашнего задания (выполнение письменных упражнений на овладение теорией), имея в виду графические представления для решения систем линейных уравнений, ставим вопрос: всегда ли система двух линейных уравнений имеет решение и всегда ли это решение можно найти графическим способом. Как удостовериться в этом, ведь даже если решение есть, но точка значительно удалена от начала отсчета после построения графика, ее можно и не увидеть. Поэтому необходимо «изобрести» точный метод для проверки есть ли вообще в системе развязки, и если есть, то сколько их может быть.
IV. Актуализация опорных знаний
Выполнение устных упражнений
1. Какие из формул задают линейную функцию:
1) у = 12х - 10; 2) у = 4 - 0,5 х; 3) у = 15х; 4) у = х(1 - х); 5) у = 11; 6) 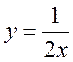 ; 7)
; 7) 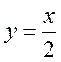 ?
?
2. Среди функций: у = х + 0,5; у = -0,5 х + 4; у = 5х - 1; у = 0,5x + 1; 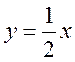 выберите те, графики которых параллельны графику функции у = 0,5 х + 1.
выберите те, графики которых параллельны графику функции у = 0,5 х + 1.
3. Выразите переменную у через переменную х в уравнении:
1) 7х - 2у = 6;
2) у - х2 = 9;
3) 3х + 0у = 5;
4) 1,5 в + 0х = 5;
5) 4х - у = 0.
V. Изучение нового материала
@ Исследование числа решений системы двух линейных уравнений с двумя переменными на основе графических представлений и знаний, свойств графиков линейных функций является основной дидактической целью урока.
После повторения вопросов: а) что является графиком линейной функции; б) условие различных случаев взаимного расположения графиков двух линейных функций и в) как из линейного уравнения выразить у через х (см. предыдущий этап урока) учащимся можно предложить практические задания.
1. В каждом из уравнений системы 1) - 3) выразите у через х и, используя представления о свойствах взаимного расположения графиков двух линейных функций, определите (не выполняя построения), взаимное расположение графиков двух линейных уравнений:
1) 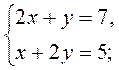 2)
2) 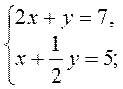 3)
3) 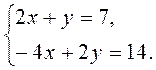
2. За взаимным расположением графиков определите количество решений системы.
3. Найдите отношение коэффициентов 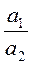 ,
, 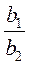 ,
, 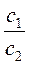 (уравнений каждой системы) и сравните их между собой.
(уравнений каждой системы) и сравните их между собой.
4. Сравните результаты выполнения п. С выводами п. 2. Сформулируй то вывод.
После выполнения и обсуждения результатов обобщаем и корректируем выводы и вносим соответствующие записи в тетради.
Конспект 22 |
Количество решений системы линейных уравнений |
Пусть дана система 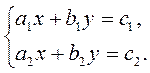 |
1) Если, 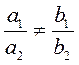 то система имеет одно решение (графики уравнений пересекаются). то система имеет одно решение (графики уравнений пересекаются). |
2) Если 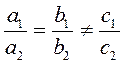 , то система не имеет решений (графики уравнений параллельные). , то система не имеет решений (графики уравнений параллельные). |
3) Если 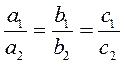 , то система имеет множество решений (решением системы является любое решение каждого из уравнений) (графики совпадают) , то система имеет множество решений (решением системы является любое решение каждого из уравнений) (графики совпадают) |
VI. Закрепление знаний, выработка умений
Выполнение устных упражнений
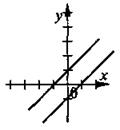
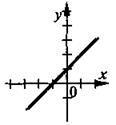
1. Сколько решений имеет система, графики уравнений которой изображены на рис., если на рис. 2) прямые параллельны, на рис. 3) совпадают?
2. Найдите отношение коэффициентов системы линейных уравнений 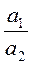 ,
, 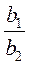 ,
, 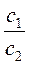 и сравните эти отношения.
и сравните эти отношения.
1) 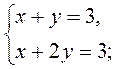 2)
2) 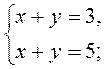 3)
3) 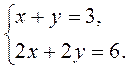
Выполнение письменных упражнений
1. Сколько решений имеет система уравнений:
1) 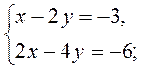 2)
2) 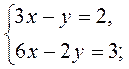 3)
3) 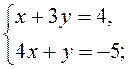 4)
4) 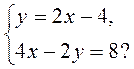
2. При каких значениях а система 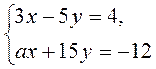
1) имеет бесконечно много решений? Найдите две такие развязки;
2) имеет одно решение? Найдите такое решение;
не имеет решений?
3. При каких значениях коэффициентов а и b решением системы уравнений 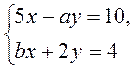 является пара чисел (2; -1)?
является пара чисел (2; -1)?
VII. Итоги урока
Среди уравнений 2х + у = 3; 2х + 2у = 6 и 2х + 2у = 3 выберите такое, чтобы вместе с уравнением х + у = 3 они образовали систему, имеющую:
1) одно решение; 2) множество решений; 3) не имеет решений.
VIII. Домашнее задание
№ 1. Выясните, имеет ли система решения и сколько. Для систем, имеющих одно решение, отыщите его, построив графики уравнений:
1) 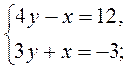 2)
2) 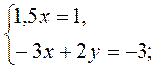 3)
3) 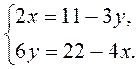
№ 2. Найдите какие-нибудь три решения системы:
1) 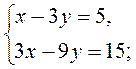 2)
2) 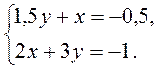
№ 3. На прямой, являющейся графиком уравнения 4х + 9у = 1, взято точку, ордината которой равна 1. Найдите абсцису этой точки.
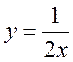 ; 7)
; 7) 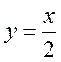 ?
?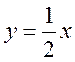 выберите те, графики которых параллельны графику функции у = 0,5 х + 1.
выберите те, графики которых параллельны графику функции у = 0,5 х + 1.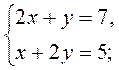 2)
2) 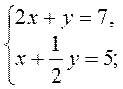 3)
3) 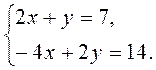
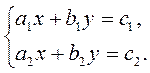
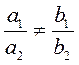 то система имеет одно решение (графики уравнений пересекаются).
то система имеет одно решение (графики уравнений пересекаются).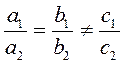 , то система не имеет решений (графики уравнений параллельные).
, то система не имеет решений (графики уравнений параллельные).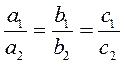 , то система имеет множество решений (решением системы является любое решение каждого из уравнений) (графики совпадают)
, то система имеет множество решений (решением системы является любое решение каждого из уравнений) (графики совпадают)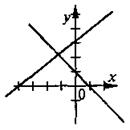
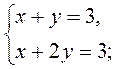 2)
2) 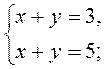 3)
3) 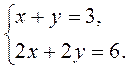
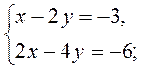 2)
2) 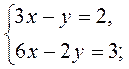 3)
3) 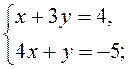 4)
4) 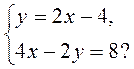
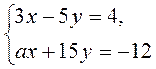
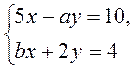 является пара чисел (2; -1)?
является пара чисел (2; -1)?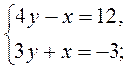 2)
2) 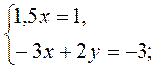 3)
3) 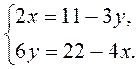
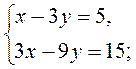 2)
2)