Часть 2 МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Раздел 7 ОСНОВЫ ТЕРМОДИНАМИКИ

7.9. Энтропия

Рассмотрим идеальную тепловую машину, что работает по циклу Карно. Для вычисления ее КПД воспользуемся соотношением (7.18) и сделаем следующие преобразования:

Кроме того, КПД такой машины можно определить по формуле (7.19):

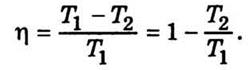
Приравнивая правые части этого выражения и выражения (7.20), получим

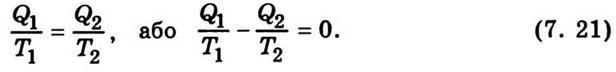
Отношение 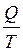называют сводной теплотой. Формулу (7.21) можно прочитать так: если система выполняет обратимый процесс, который графически изображается в виде отрезков двух изотерм и двух адіабат, то алгебраическая сумма суммарных теплот равна нулю. Нескінченка малым отрезкам изотерм соответствуют бесконечно малые количества теплоты δQ. Следовательно, для суммы суммарных теплот для обратимого процесса получим такое соотношение:

Кружочек на интеграле означает, что интеграл берется по замкнутому контуру, который изображает процесс. Следовательно, для вычисления интеграла (7.22) надо знать диаграмму процесса. Формула (7.22) является количественным выражением второго принципа термодинамики. Однако эту формулу можно применить только к оборотных циклов.

Чтобы получить общее выражение второго принципа термодинамики, который можно применить к любому термодинамического процесса, надо прежде всего ввести понятие о новую физическую величину, которую называют энтропией. В 1865 г. в физике это понятие ввел Г. Клаузиус.

Введем функцию состояния системы S, изменение которой при переходе системы из состояния 1 в состояние 2 определяется интегралом 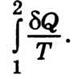Эту функцию называют энтропией. Если энтропию в состоянии 1 обозначить S₁, а в состоянии 2 - S₂, то изменение энтропии при переходе из состояния 1 в состояние 2 будет

Для бесконечно малых изменений энтропии можно записать

Энтропия является функцией состояния системы, и в этом нетрудно убедиться. Рассмотрим два состояния системы 1 и 2, представленные на рис. 7.6. Применим второй принцип к обратимому процессу 1А2В1:

Запишем этот интеграл как сумму двух интегралов:

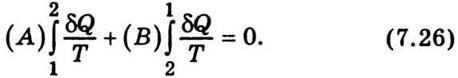
Если же система перешла из состояния 1 в состояние 2 путем 1С2В1у то можно записать

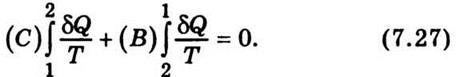
В выражениях (7.26) и (7.27) одно слагаемое совместный, поэтому

Из выражения (7.28) видно, что энтропия системы при обратимом процессе не зависит от пути перехода из одного состояния в другой. Можно показать, что при переходе системы из одного состояния в другое при необратимом процессе сумма суммарных теплот 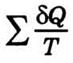меньше от изменения энтропии dS. Для элементарного необратимого процесса

Следовательно, общее выражение второго принципа термодинамики имеет следующий вид:

где знак равенства касается обратимых процессов, а знак неравенства - необратимым.

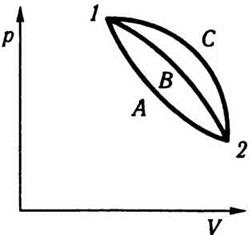
Рис. 7.6

При переходе системы из одного состояния в другой энтропия может увеличиваться или уменьшаться в зависимости от того, достает система теплоту, отдает ее. При плавлении тела энтропия увеличивается, при кристаллизации уменьшается; при испарении увеличивается, при конденсации - уменьшается.

Если система состоит из нескольких тел и во время процесса энтропия одного из них изменяется на ΔS₁, второго на ΔS₂, третьего на ΔS₃ и т. д., то изменение энтропии системы будет

Энтропия является величиной аддитивной, то есть энтропия системы равна алгебраической сумме энтропий тел, входящих в состав системы. Отсюда следует, что во время процесса изменение энтропии может равняться нулю, то есть энтропия системы может оставаться постоянной. Предположим, что система полностью изолирована. Тогда она изолирована в тепловом отношении, теплообмена нет, то есть δQ = 0. Если в этой системе происходят обратимые процессы, то

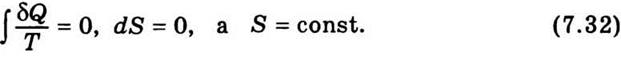
Следовательно, энтропия изолированной системы, в которой происходят обратимые процессы, остается постоянной. Если в изолированной системе происходят необратимые процессы, то согласно (7.29)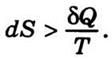

Поскольку в изолированной системе процессы происходят адиабатически и δQ = 0, то

Т.е. при необратимом процессе в изолированной системе энтропия системы возрастает.

Поскольку все реальные процессы необоротные, мы приходим к выводу: в замкнутых системах все процессы происходят в направлении роста энтропии. Когда наступает равновесие, процессы прекращаются и энтропия достигает наибольшего из возможных значений. Следовательно, с точки зрения термодинамики получается, что условием равновесия в замкнутой системе является максимум энтропии. Это дало основание Г. Клаузіусу сформулировать второй принцип термодинамики так: энтропия любой изолированной системы стремится к максимуму.

Если закон возрастания энтропии (второй принцип) указывает на направление течения процессов, то закон сохранения энергии (первый принцип) указывает на то, как должен происходить тот или иной процесс.

Второй принцип утверждает, что во всех изолированных системах энтропия остается постоянной при обратимых процессах или увеличивается при необратимых. Поскольку полностью обратимые процессы являются предельным идеализированным случаем, то фактически во всех замкнутых системах энтропия возрастает, в чем проявляется приближение системы к термодинамического равновесия.

Следует отметить, что изменения в системе в направлении статистической равновесия присущие только изолированным системам. Если система незамкнутая, то в ней не может наступить статистическое равновесие. Например, жизнь на Земле постоянно развивается, и живые организмы не обнаруживают тенденции к переходу в состояние с максимальной энтропией. Однако это не означает, что процессы в организмах противоречат второму закону термодинамики или организмы «антиентропійними» системами. Второй принцип с его требованием о необходимости статистической равновесия можно применять только в замкнутых систем, организмы есть же незапертой, или открытыми системами. Они постоянно взаимодействуют с окружающей средой, получая от него продукты питания, воздух, свет, теплоту. Относительно таких систем второй принцип не содержит в себе никаких утверждений. Если же организм полностью изолировать от окружающей среды и превратить его в замкнутую систему, то понятно, что без воздуха и обмена веществ он очень быстро перейдет в состояние термодинамического равновесия со средой. Следовательно, тенденция к дезорганизации и неупорядоченного движения превалирует в замкнутых системах, тогда как в незамкнутых системах, для которых характерен высокий уровень организации, возможен как угодно долго упорядоченное движение и развитие по восходящей линии. Такие системы принято характеризовать негентропією, которая, по физической сути связана с энтропией и для открытых систем также растет со временем.