Формулы сокращенного умножения

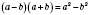
- формула разности квадратов.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
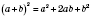
- формула квадрата суммы.
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение этих выражений плюс квадрат второго выражения.
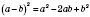
- формула квадрата разности.
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение этих выражений плюс квадрат второго выражения.
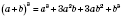
- формула куба суммы.
Куб суммы двух выражений равен кубу первого выражения плюс утроен произведение квадрата первого выражения и второго, плюс утроен произведение первого выражения и квадрата второго плюс куб второго выражения.
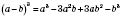
- формула куба разности. (Читается аналогично предыдущей формуле.)
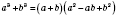
- формула суммы кубов.
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
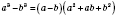
- формула разности кубов.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Формулы сокращенного умножения применяются для тождественных преобразований, в частности для разложения многочленов на множители.
Примеры
1) Упростить выражения:
а)
;
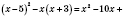
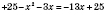
б)

.
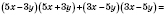
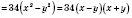
2) Решить уравнение:
а) ,
,
,
, ;
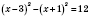
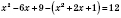
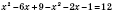
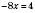
б) ,
,
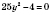
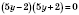
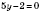
или ,
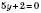
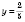
или .
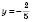
3) Разложить на множители:
а) ;
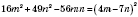
б) ;
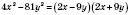
в)


.
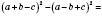
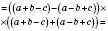
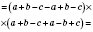
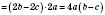
4) Найти наименьшее значение выражения:

.
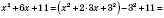
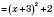
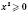
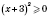
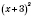
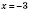
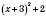
Учитывая, что для любых значений х, получаем, что для любых значений х. Наименьшее значение равно 0, если . Следовательно, наименьшее значение равно 2 при .
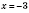