Урок № 69
Тема. Уравнение с двумя переменными и его решение
Цель: сформировать представление об уравнении с двумя переменными и его решения; уяснить содержание понятия «график уравнения с двумя переменными»; выработать умения: отбирать проверкой решения уравнения с двумя переменными; работать с готовым графиком уравнения с двумя переменными; преобразовывать уравнение вида у = f(x) и вычислить решение уравнения с двумя переменными.
Тип урока: усвоение новых знаний.
Ход урока
I. Организационный момент
II. Проверка домашнего задания
@ Учитель собирает тетради, чтобы проверить качество коррекционной работы учащихся и творческое задание.
III. Актуализация опорных знаний
Выполнение устных упражнений
1. Решите уравнение:
3х = 6; 3х + 2 = 6; 6х = 3; 6 + х = 3; 6 + x = 2x - x + 6, 3х + 5 = 3х + 7.
Что значит «решить уравнение»?
2. Составьте уравнение по условию задачи:
1) длина прямоугольника х, ширина 3 м, а периметр 20 м;
2) ширина прямоугольника х, длина на 4 м больше, а периметр 20 м;
3) ширина прямоугольника х, длина в м, а периметр 20 м.
Если можно, решите уравнение, найдите длины сторон прямоугольника.
3. Принадлежит ли графику функции у = 3х + 2 точка А(1; -5); В(3;11); С(0; 2)? Почему?
4. Является ли данное равенство правильной: 2 · 1 + 3 · (-1) = 5; 2 · 0,5 + 3 · (-1) = -2?
IV. Формулировка цели и задач урока
После повторения основных понятий, изученных в теме «Линейные уравнения с одной переменной», и выполнение устных упражнений и составление уравнений вместе с учащимися формулируем цель: познакомиться с тем новым видом уравнения, что встретился нам во время решения одной из задач.
V. Изучение нового материала
@ Новое понятие «уравнение с двумя переменными» вводится на примерах (так же, как и «уравнения с одной переменной»), а затем формулируется определение уравнения с двумя переменными и определение решения такого уравнения, как упорядоченной пары чисел - значений переменных, которые превращают уравнение в верное равенство, так же, как и корень уравнения с одной переменной. Это определение должно быть хорошо понятным всем ученикам. Понятие равносильных уравнений с двумя переменными строится на известных учащимся понятие равносильных уравнений и свойства равносильных уравнений. И вообще, автор считает, что формирование новых знаний учащихся будет более результативным, а знания - более сознательными, если во время изучения нового материала обратиться к приему аналогии (уравнение с одной переменой). Из этого выпадает только понятие графика уравнения с одной переменной, но это является исключением, что подтверждает справедливость правила. Поэтому и записи в тетрадях учащихся могут иметь вид сравнительной таблицы, в которой выделены ключевые слова.
Конспект 21 |
Вид утверждения |
Уравнения с одной переменной |
Уравнения с двумя переменными |
1) Пример |
х + 5 = 8 |
х + у = 8 |
2) Описание |
Равенство, содержащее неизвестное число, обозначенное буквой (переменная) |
Равенство, содержащее два неизвестных числа, обозначенных буквой (переменные) |
3) Сопутствующие понятия |
Корень уравнения с первой переменной - значение переменной, превращает уравнение в верное равенство |
Решение уравнения с двумя переменными - упорядоченная пара чисел (х;у), при которых уравнение превращается в верное равенство |
4) Равносильны |
уравнения с одной переменной - имеют одинаковые корни или не имеют корней |
уравнения с двумя переменными - имеют одни и те же решения или оба не имеют решений |
5) Свойства равносильных уравнений |
Одинаковые |
6) График |
? |
Фигура, состоящая из точек (х; у), таких, что их координаты - решение уравнения |
VI. Закрепление материала. Выработка умений
Выполнение устных упражнений
1. Является ли решением уравнения х - 2у = 6 пар чисел(0; 0); (2; -2); (8; 1); (0; 3); (15; 4); (6; 0); (5; -5,5)?
2. Точки А(...; 0); В(0; ...); С(1; ...); D(...; -3) принадлежат графику уравнения 3х - у = 6. Найдите пропущенные координаты.
3. Выразите переменную у через переменную х (сведите уравнение к виду y = f(x)) путем выполнения тождественных преобразований: х + у = 1; 5х + 5у = 0;
х - у = 2. По заданной формуле найдите два решения каждого уравнения.
Выполнение письменных упражнений
1. Пары значений х и у, внесены в таблицу. Какие из них являются решениями уравнения 1) х2 + у2 = 25; 2) х2 - у2=7?
х |
-5 |
-4 |
-3 |
-1 |
0 |
3 |
4 |
5 |
в |
0 |
3 |
4 |
1 |
-5 |
4 |
-3 |
0 |
2. Выразите из уравнения переменную у через переменную х. Используя созданную формулу, найдите три каких-либо решения уравнения:
1) х + у = 27;
2) 2х - у = 4,5;
3) 3х + 2у = 12;
4) 5у - 2х = 1.
3. Какие из точек А(-2; -5); В(4; 1); С(1; -4); D(2; 2) принадлежат графику уравнения х2 - 2ху + у3 = 0?
4. Докажите, что уравнение:
1) х2 + у2 = -1 не имеет решений;
2) х2 + у2 = 0 имеет только одно решение.
Дополнительно. Среди решений уравнения х + 2у = 18 найдите такую пару, которая бы состояла из двух одинаковых чисел.
VII. Итоги урока
Контрольные вопросы
1. Что называется решением уравнения с двумя переменными? Есть пара (2; 1) решением уравнений: 2у - х2 = -2; 3х - у = 4; х2 - у3 = 3; ху = 3?
2. Какие уравнения с двумя переменными называют равносильными? Приведите пример.
3. Что такое график уравнения с двумя переменными?
VIII. Домашнее задание
№ 1. Изучите содержание основных понятий и составьте алгоритмы:
а) «Как проверить, есть пара (х;у) решением уравнения с двумя переменными»;
б) «Как найти решение уравнения с двумя переменными».
№ 2. Выразив переменную у через х, найдите три каких-либо решения уравнения:
1) ху - 12 = 0; 2) 3х - у = 10.
№ 3. Какие из точек А(-3; 12); В(2; -1); С(0; 3) принадлежат графику уравнения х2 - у + 3 = 0?
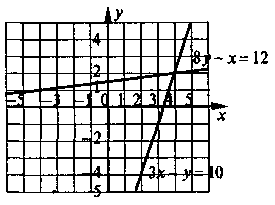
№ 4. На рисунке построены графики уравнений 3х - у = 10 и 8у - х = 12. Для каждого из уравнений найдите по его графику несколько решений. Используя рисунок, укажите такую пару чисел, которая является решением как первого, так и второго уравнения, проверьте ответ исчислением.