Часть 2 МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Раздел 7 ОСНОВЫ ТЕРМОДИНАМИКИ

7.5. Адиабатический процесс. Уравнение адиабаты

Адиабатическим называют процесс, который происходит без теплообмена системы с окружающей средой. Для осуществления адиабатического процесса надо окружить систему такой оболочкой, которая не пропускает теплоты, но мешает тому, чтобы система выполняла работу или работа выполнялась над системой. Такую оболочку называют адіабатичною. Примером оболочки, близкой к адиабатической, может быть оболочка из плохого проводника теплоты. При адиабатическом процессе система обменивается энергией со средой только в результате работы, при этом она не получает и не отдает теплоты, т.е. ΔQ = 0. Первый принцип термодинамики для этого случая и бесконечно малых величин имеет вид

где dU - полный дифференциал; δА - неполный дифференциал. Пусть моль идеального газа находится под поршнем. Закрепив поршень, повысим температуру газа на dТ. Поскольку объем газа остается постоянным, то количество теплоты, которая нужна для такого нагрева, равна С_VdТ. А поскольку при этом не выполняется работа, то эта количество теплоты равно увеличению внутренней энергии газа dU = C_VdТ.

Если начальное состояние (T, V) будет таким же, что и в предыдущем опыте, но поршень не закреплен, а может свободно перемещаться при неизменном внешнем давления р, то газ будет выполнять работу δА = рdV. Поскольку внутренняя энергия газа зависит только от температуры, то она меняется так же, как и в предыдущем случае.

Следовательно, при адиабатическом процессе система выполняет работу за счет внутренней энергии, которая связана с температурой. Изменение внутренней энергии при адиабатическом процессе приводит к изменения температуры системы. Учитывая, что ΔА = р ∆ V [см. формулу (7.2)] и ΔU =С_VΔТ, формула (7.10) наберет такого вид:

При адиабатическом расширении газа, когда увеличивается объем (ΔV > 0), из формулы (7.11) видно, что температура снижается (ΔT 0), т.е. газ охлаждается. Если же ΔV 0, то ΔТ > 0, т.е. газ нагревается. К вещи, свойство газов охлаждаться при расширении их в адіабатичних условиях положен в основу принципа действия холодильников. Следовательно, при адиабатическом процессе температура системы может варьироваться, хотя системе теплота не передается. Отсюда следует, что теплоемкость системы при адиабатическом процессе равна нулю. Однако ноль - это фиксированное число, а процесс, при котором теплоемкость остается постоянной, называют політропним. Поэтому адиабатический процесс является частным случаем політропного процесса, а именно таким політропним процессом, при котором теплоемкость равна нулю. Уравнение адиабаты идеального газа имеет такой вид:

где γ = С_г / С_V - отношение теплоемкости газа при постоянном давлении и постоянном объеме. Уравнение (7.12) называют уравнением Пуассона. Из соотношения (7.11) получим выражение для работы, если система адиабатически переходит из одного состояния в другое:

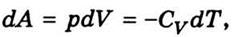
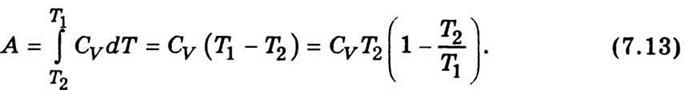
Можно показать, что для адиабатического процесса

Заменив в (7.13) отношение температур отношением объемов согласно (7.14), получим выражение для работы при адиабатическом расширении идеального газа