СТРОЕНИЕ АТОМА

6. Волновая модель

Противоречивость теории Бора удалось устранить с помощью представленных Е. Шредингером и В. Гейзенбергом представлений, сохраняя при этом основную идею теории квантов:

♦ предположение о движении электрона с определенной скоростью по постоянной орбите противоречит принципу неопределенности Гейзенберга. Данный принцип утверждает, что невозможно абсолютно точно определить одновременно положение и скорость электрона;

♦ электронный отводится какая-то определенная орбита, а пространство, в котором он может находиться, так называемая электронная облако;

♦ электронная облако является трехмерным пространством местонахождение электронов, которые, по Шредингером, можно описать математическими функциями (волновыми функциями);

♦ квадрат волновой функции определяет вероятность нахождения электрона в облаке.

Запомните: орбиталь является ограниченным пространством, в котором вероятность нахождения электрона максимальная (примерно 90 %).

6.1. Основные свойства волновой модели

Для описания энергетических уровней электрона в дополнение к теории Бора используют четыре квантовых числа.

♦ Главное квантовое число n обозначает энергетический уровень электронной орбитали. Оно соответствует номеру электронной оболочки в атоме и совпадает с периодом, в котором находится элемент в периодической системе.

♦ Побочное квантовое (орбитальное) число l характеризует разницу энергий внутри одного энергетического уровня и пространственную форму орбитали.

♦ Магнитное квантовое число m определяет пространственную ориентацию электронных орбиталей атома под влиянием внешнего магнитного поля.

♦ Спінове квантовое число s учитывает различные собственные направления вращения электронов, так называемый спин.

Четыре квантовых числа могут приобретать только определенных значений, которые отвечают так называемым правилам отбора.

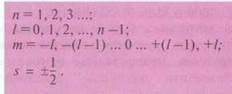
Четыре квантовых числа однозначно описывают каждый электрон атома. Это можно сравнить с однозначно закрепленными телефонными номерами, никогда не повторяются.

В отношении электронов в одном атоме В. Паули сформулировал в 1925 г. принцип, названный его именем, принцип Паули:

электроны атома должны отличаться между собой, как минимум, одним квантовым числом.

Запомните: на каждой орбитали могут находиться два электрона с разным спином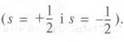

Комбинация всех четырех квантовых чисел для n = 1 - 3 обуславливает такую населенность электронов:

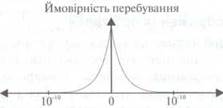
Орбитали с побочным квантовым числом l = 0 имеют сферически-симметричную пространственную структуру, вероятность пребывания электронов внутри орбитали больше вблизи атомного ядра, и по мере удаления от атомного ядра она уменьшается.

Запомните: орбитали с l = 0 называют s-орбіталями.

Орбитали с побочным квантовым числом l = 1 имеют пространственную структуру в форме гантели. Согласно правилам отбора существуют три возможных магнитных квантовых числа со значениями -1, 0, +1. Им соответствуют три орбитали в трех направлениях.

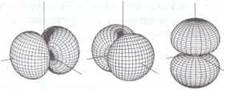
Запомните: орбитали с l = 1 называют г-орбіталями.

Орбитали с побочным квантовым числом l = 2 имеют пространственную структуру в форме розетки. Согласно правилам отбора получаем пять возможных магнитных квантовых чисел со значениями -2, -1, 0, +1, +2. Им соответствуют пять орбиталей.

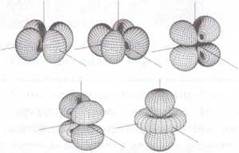
Запомните: орбитали с l = 2 называют d-орбіталями.