Урок № 68

Тема. Сравнение рациональных чисел

Цель: на основе наблюдений и опыта учащихся вывести правило сравнения любых двух рациональных чисел и выработать умение использовать его для сравнения рациональных чисел и решения упражнений, предполагающих сравнение рациональных чисел.

Тип урока: применение знаний, умений и навыков.

Ход урока

I. Проверка домашнего задания

@ По мнению автора, чтобы сэкономить время, надо проверить только № 3, 4, 5 (особенно обращаем внимание на использование свойств умножения и сложения для упрощения вычислений в № 5). Все остальное проверяем, собрав тетради учеников.

II. Актуализация опорных знаний

Устные упражнения

2. Назовите числа, противоположные числам: 15; -3; -38; 0; a; c+d.

3. Найдите модули чисел: 13; -8; -615; 0; а, если а - положительное, b, если b - отрицательное.

4. Решите уравнение: |х| = 3; |t| = 0,4; |в| = ; |u| = 0.

5. Поставьте вместо * знак «>» или «», чтобы запись была правильным: 35* 0,35; 35,1* 35,01; *; 2,7 * 2.

III. Применение знаний

1. Сравнение чисел с помощью координатной прямой

Задача. Отметьте на координатной прямой числа 2; 5; 7; 4. Сравните числа: а) 2 и 5; б) 2 и 7; в) 2 и 4. Выясните с помощью координатной прямой, как расположено число 2 по отношению к каждому из других чисел.

@ Видим, что 2 слева от 5; 2 слева от 7, 2 слева от 4. Вспомним, что в 5 классе во время изучения темы сравнения натуральных чисел мы говорили, что на координатном луче меньше число всегда лежит слева, а больше - наоборот - справа. Вообще, на координатной прямой больше двух чисел лежит справа, а меньше - слева.

Пример. Сравните числа a, b, c, d, изображенные на рисунке (запишите в порядке возрастания).

Решения. b c a d, поскольку слева направо числа идут именно в таком порядке.

2. Правило сравнения рациональных чисел
Обратимся к координатной прямой.

Мы видим, что все положительные числа лежат справа от 0, а все отрицательные числа слева от 0, следовательно:

1) положительное число больше 0; отрицательное число меньше 0;

2) любое положительное число больше любого отрицательное число.

Например, 3 > 0; -3 0; -3 3; 3 > -3.

Если же оба числа (а и b) отрицательные (см. рис), то

слева будет то число, которое далее за другое от 0, а следовательно:

3) из двух отрицательных чисел больше то, у которого модуль меньше.

Например, -3,7 > -7,3, поскольку|-3,7| = 3,7; 3,7 7,3, поскольку |-7,3| = 7,3.

3. Вывод. Рациональные числа можно сравнивать как с помощью координатной прямой, так и с помощью правил сравнения. В первом случае: больше то число, которое лежит справа.

Во втором случае:

а) положительное > отрицательного; б) положительное > 0; в) отрицательное 0; г) из двух отрицательных чисел больше то, у которого модуль меньше.

@ Вопрос символической записи этих правил не решаются однозначно и способ его решение зависит от подготовки учащихся.

IV. Усвоение умений

@ Так много времени на этом уроке потрачено на объяснение нового материала, времени на различные по содержанию и уровню упражнения не хватит. Поэтому главная цель - хорошо отработать применение правил сравнения рациональных чисел на стандартных упражнениях.

Устные упражнения

1. Прочитайте неравенства. Являются ли они правильными?

а) 0 3; б) 0 > -5; в) -7 0; г) -3 > 2; д) -7 1; е) -2 -5; ж) -5 -3.

2. Известно, что а b с. Какой из рисунков соответствует этому условию?
1) 2) 3) 4)

Письменные упражнения

1. Поставьте вместо * знак «>» или «», чтобы образовалась правильная неравенство:

а) 8,9 * 9,2;

б) -240 * 3,2;

в) 4,5 * -800;

г) -5,5 * -7,2;

д) -96,9 * -90,3;

есть) -100 * 0;

ж) -1000 * 0;

с) *;

к) *.

2. Расположите в порядке возрастания следующие числа:

1) -4; 3; -2; 1; 0; -1; 2; -3; 4;

2) -5,4; 4,3; -3,2; 2,1; -1,2; 2,3; -3,4.

3. Какое из чисел -5; -1; 8; 0; -5,3 больше всего? меньше? В которого из них наибольший модуль? наименьший модуль?

4. Заполните таблицу. Для этого в каждую ячейку впишите число, которое удовлетворяет оба условия:

5. Известно, что х и у - положительные числа, а т и п - отрицательные. Сравните:
а) 0 и n; б) в и 0; в) -х и 0; г) 0 и -m; д) х и т; е) n и х; ж) -m и n; с) -х и у; к) |m| и m; л) -|m| и m; м) х и |х|; н) x и |-х|.

Дополнительно. Упражнения на повторение

6. Какие числа имеют модуль, равный 2; 1,7; 5; 0; 1; -(-4)?

7. Определите координаты точек В, С и Д если A(т) (см. рис).

8. Найдите неизвестный член пропорции: а) 3,5 : x = 0,8 : 2,4; б) 6,8 : 2,5 = х : 1,5.

V. Итог урока

Вопрос к классу

1. Какое число больше:

· положительное или отрицательное;

· положительное или 0;

· отрицательное или 0;

· а или b, если а и b - отрицательные и |а| > |b|?

2. Известно, что а 0; b > 0; c > b. Назовите числа в порядке их расположения на координатной прямой слева направо.

VI. Домашнее задание

1. Поставьте вместо * знак «>» или «» так, чтобы образовалась правильная неравенство:

а) -3542 * -2763; б) -65,43 * -65,39; в) - * -0,7; г) -1,16 * ; д) -* -; е) -0,8 * .

2. Расположите числа 2,8; 0,5; 0; -1; -1,1; 0,1 и -1,6:
а) в порядке возрастания; б) в порядке убывания.

3. Вычислите .

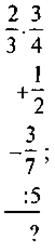
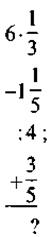
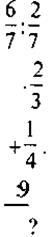
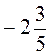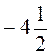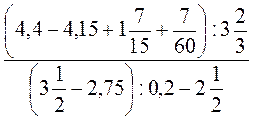4. Найдите неизвестный член пропорции : 3,1 = х : 9,3.