|
В. Работы учеников проверяем выборочно, в основном в «слабых», все остальные сверяют ответы.
II. Применение навыков @ На этом уроке решаем упражнения более высокого уровня сложности (обобщающие и исследовательские) и повторяем понятия положительного, отрицательного числа, «рациональные числа», «модуль числа». 1. Между какими соседними целыми числами стоит число? а) -2,73; б) -9,5; в) -0,63; г) 0,87; д) -1 Ответ запишите в виде двойного неравенства. 2. Какие цифры можно записать вместо *, чтобы образовалась правильная неравенство: а) -3841 -384*; б) -*5,44 > -25,44; в) - 3. Запишите в виде неравенства предложение: а) -4,3 - отрицательное число; б) 27,1 - положительное число; в) а - отрицательное число; г) b - положительное число; д) * с - неотрицательное число; есть) * d - недодатне число. 4. Игровой момент
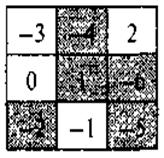
Ученик, которого вызвали к доске, называет и показывает по очереди то «красные», то «синие» числа, записанные в таблице. При этом «красные» называет числа в порядке возрастания, а «синие» - в порядке убывания, то есть называет числа в такой последовательности: -6; 2; -5; 0; -4; -1; -2; -3; 1. Если ученик ошибся, то садится на место, и к доске идет другой.
III. Диагностика усвоения знаний и умений Самостоятельная работа Вариант 1 1. Начертите координатную прямую с единичным отрезком 1 см. Отметьте на координатной прямой: а) точки A(2); B(-3,5); C(-1); D(-2); Е б) точку K в) точки, модули координат которых равны 5; 4,5; 0. 2. Даны числа: 6; -9; 5,25; 2 а) Какие из данных чисел являются: натуральными? целыми? дробными? положительными? отрицательными? б) Найдите модули этих чисел. Какие из данных чисел имеют равные модули? Почему? в) Расположите числа в порядке возрастания.
Вариант 2 1. Начертите координатную прямую с единичным отрезком 1,5 см (3 ячейки). Отметьте на этой прямой: а) точки M(2), N б) точку А в) точки, модули которых равны 4; 1 2. Дано числа: 0; 7; -11; -3,8; 4 а) Какие из данных чисел являются: натуральными? целыми? дробными? отрицательными? б) Найдите модули этих чисел. Какие из них имеют равные модули? Почему? в) Расположите числа в порядке убывания.
IV. Итоги урока Проверяем качество выполнения самостоятельной работы. Анализируем ошибки.
V. Домашнее задание 1. Сравните числа и результат запишите в виде неравенства: а) - 2. Расположите числа 5; -9; 0; 0,88; -6,9; 8,92 в порядке убывания. 3. * Проверьте справедливость неравенств 1) |a + b| ≤ |a| +|b|; 2) |a - b| ≤ |a| + |b|; 3) |a| - |b| ≤ |a + b|; 4) |a| - |b| ≤ |a - b|; 5) |а| - |b| ≤ |a| + |b|. при таких значениях букв:
а) а = -7; b = -5; б) а =
|
|
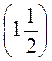 ;
; 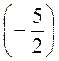 и точку
и точку 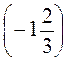 , Р(-1), К
, Р(-1), К