Степень с натуральным показателем
Степенью числа
a с натуральным показателем
n, большим 1, называется произведение
n множителей, каждый из которых равен
a. Т.е.
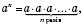
где a - основание степени;
n - показатель степени.
Степенью числа
a с показателем 1 является само число
a.
Знак степени с натуральным показателем
1. Если основание степени
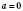
, то
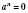
для любого натурального значения
n.
2. Если
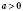
, то
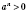
для любого натурального значения
n.
3. Если
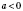
и
n - число четное, то
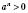
. Например:
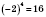
;
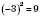
;
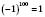
.
Если
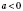
и
n - нечетное число, то
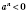
. Например:
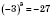
;
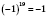
.
Свойства степени
1. При умножении степеней с одинаковыми основаниями оставляют ту же основу, а показатели степеней добавляют:
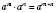
для любого числа
a и произвольных натуральных чисел
m и
n.
2. При подъеме степени в степень основание оставляют ту же, а показатели степеней перемножают:
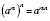
для любого числа
a и произвольных натуральных чисел
m и
n.
3. При делении степеней с одинаковыми основаниями оставляют ту же основу, а из показателя делимого вычитают показатель делителя:
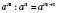
для любого числа
a и произвольных натуральных чисел
m и
n таких, что
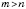
.
4. Чтобы возвести в степень произведение, достаточно поднести к этому степень каждый множитель и результаты перемножить:
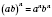
для любых чисел
a,
b и произвольного натурального числа
n.
5. Чтобы возвести в степень долю, нужно поднести к этому степень делимое и делитель, а потом поделить степень делимого на степень делителя:
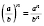
для любых чисел
a и
b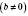
и произвольного натурального числа
n.