Урок № 5
Тема. Сложение и вычитание дробей
с одинаковыми знаменателями
Цель. Углубить знания учащихся о
дробь; учить прибавлять и вычитать дроби с одинаковыми знаменателями. Развивать
вычислительные навыки, культуру математической речи и записей.
Воспитывать самостоятельность, интерес к математике.
Тип урока: усвоение новых знаний.
Оборудование: карточки с числами,
таблицы: „Сложение дробей с одинаковыми знаменателями”, „Вычитание дробей с
одинаковыми знаменателями”.
Ход урока
И. Организационный момент.
II. Проверка домашнего задания.
1. Ученики-консультанты после проверки
домашнего задания отчитываются о состоянии его выполнения.
2. „Микрофон”.
а) Назвать правильные дроби с
знаменателем 9;
б) Назвать неправильные дроби с
знаменателем 9;
в) Какой из дробей больше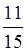 
ли 
?
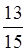г) Какой из дробей меньше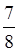 
ли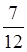 
?
III. Актуализация опорных знаний.
Устный счет:
1.
Найти сумму
чисел 275 и 34.
2.
Найти разницу
чисел 156 и 45.
3.
От суммы чисел
34 и 165 отнять 56.
4.
К разности чисел
89 и 45 добавить 96.
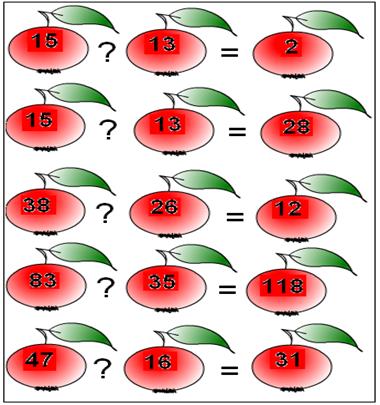
Игра „Распознай действия”
Учитель раскрывает магнитную доску с карточками,
на которых написаны числа, между которыми нужно поставить действия.
Таблица № 1 „Распознай действия”
ИV. Формирование новых знаний.
Учитель обращает внимание учащихся на
таблицу.
Таблица 2. „Сложение дробей с
одинаковыми знаменателями”
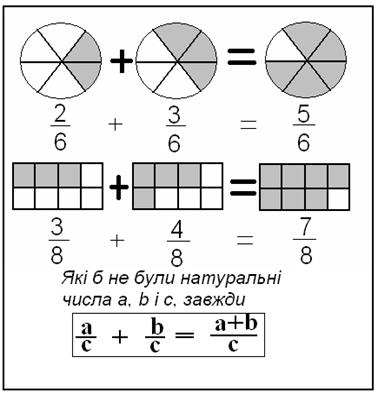
Подвести учащихся к самостоятельному
заключения относительно сложения дробей с одинаковыми знаменателями. Если первая дробь
записать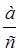 
, а второй - 
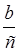, то получим сумму: +=
.
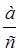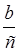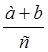Например,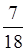 
+
=
=
.
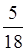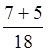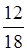Далее предлагаю учащимся рассмотреть
следующую таблицу
Таблица 3. „Вычитание дробей с
одинаковыми знаменателями”
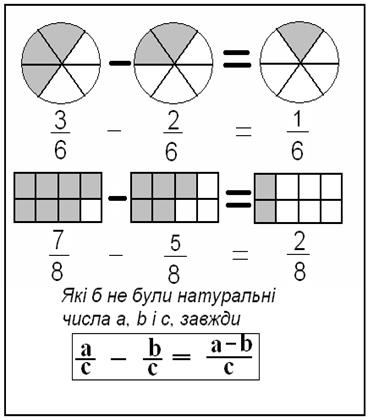
Например,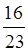 
-
=
=
.
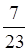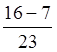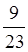Обращаю внимание учащихся, что вычитание
возможно только при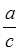 
> 
.
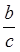Поскольку одинаковые
знаменатели прошу учеников сравнить числа.
Вывод записываем
вместе, что а > b.
Далее предлагаю учащимся
добавить в одного яблока его половину, третью часть, четвертую.
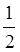1+
=1;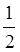 
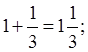
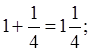
Учу детей как читать такие
числа. Обращаю внимание детей на название, это смешанные числа.
Каждое смешанное число имеет целую и
дробную части. Дробная часть - дробь правильный.
В приведенном примере целая часть -
число 2, а дробная -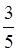 
. Поскольку 2=
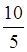, то 2=+=
.
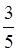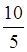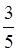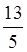Каждое смешанное число равно
некотором неправильном дроби с тем же знаменателем. Чтобы найти числитель этого
дроби, надо целую часть смешанного числа умножить на его знаменатель и к
результату прибавить числитель дробной части.
Например, чтобы превратить в
неправильный дробь смешанное число 3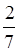
, пишем: 3 = 
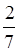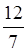. Устно
находим: 37 + 2 = 23.
Следовательно, 3 =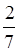 
.
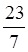Каждый неправильный дробь
равна или натуральном или смешанном числу. Если числитель неправильной
дроби делится без остатка на знаменатель, то дробь равна их доле.
Например,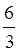 
=2, т.к. 6 : 3=2; 
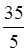=7, 35 : 5=7.
Если же при делении числителя
на знаменатель неправильной дроби образуются неполная доля и остаток, то
неполная доля - это целая часть смешанного числа, а остаток - числитель его
дробной части. Например,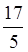 
=3
,
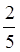поскольку 17 : 5 = 3 (ост. 2).
Физкультминутка
Все подняли руки - раз!
На пальчиках стоит весь класс,
Два - присели, руки вниз,
На соседа посмотри.
Раз! - и вверх,
Два! - и вниз,
На соседа не смотри.
Будем дружно мы прыгать,
Чтоб ногам работу дать.
V. Формирование умений
1. Выполним вместе. Устный счет. №
1001.
2. Работа по уровням.
И уровень №
1007.
II уровень № 1008.
III уровень № 1010, № 1011.
ИV уровень№ 1013, № 1014, № 1015, № 1016, № 1053.
Ученики i И II уровня берут
консультацию у учителя и у учеников ИV
уровня. Ученики III иV уровня консультируются между собой и с
учителем.
ИV. Итог урока
Историческая справка.
VII. Домашнее задание
§ 22; И уровень № 1006, II уровень №
1009, III уровень № 1012, VИ уровень № 1017.