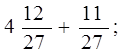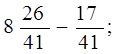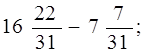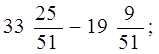Урок № 6

Тема. Решение задач и упражнений на сложение и вычитание дробей с одинаковыми знаменателями

Цель урока. Отрабатывать и совершенствовать навыки решения’увязки задач. Предусматривающие выполнение действий сложения и вычитания дробей с одинаковыми знаменателями. Развивать культуру математической речи и записей. Воспитывать способности к математики.

Тип урока: применение навыков и умений.

Оборудование: карточки с заданиями, таблицы: „Сложение дробей с одинаковыми знаменателями”, „Вычитание дробей с одинаковыми знаменателями”, „Найти сумму”, „Найти разницу”.

Ход урока

И. Организационный момент

II. Проверка домашнего задания

Выяснить, какие трудности возникли в учащихся во время выполнения домашнего задания. Собрать тетради на проверку.

III. Актуализация опорных знаний.

На доске изображены таблицы с которыми работают ученики.

1. Найти сумму:

2. Найти разницу:

ИV. Совершенствование умений

1. Выполнить устно. № 1002, № 1004, № 1005.

2. Работа в группах.

Класс поделен на 3 группы. В каждую группу входят ученики разных уровней.

Ученики ИV уровня - это консультанты. Группы получают карточки.

Задачи И группы:

Выполнить действия:

а) ++; б)

Задания II группы:

Выполнить действия:

а) - - ; б)

Задача III группы:

Выполнить действия:

а) б)

Закончив работу каждая группа обсуждает результаты с учителем. Затем представитель от группы записывает решение на доске и объясняет его.

Физкультминутка

Сел мотылек на травку

И считает рахівничку:

1, 2, 3 - ты бабочке лети.

Крылышки уже за головой

Поэтому смотри перед собой.

Выпрямляем позвоночник,

Крылышки сводим вперед,

Словно бабочки, літаєм,

Крылышки зводим, розправляєм.

3. Решения упражнений.

а) Учащиеся i И II уровня работают вместе.

1). „Делай как я”.

№ 1019 (а)

2). Комментируемое выполнения № 1019 (б)

3). Самостоятельное выполнение с проверкой № 1019 (в).

б) Учащиеся III уровня, консультируясь с учениками-консультантами и учителем выполняют № 1020, № 1022;

в) Ученики ИV уровня консультируются с учителем № 1023 (а).

Самостоятельно выполняют № 1023 (в), № 1024, № 1051.

V. Итог урока

1. Как добавить дроби с одинаковыми знаменателями?

2. Как вычесть дроби с одинаковыми знаменателями?

3. Пользуетесь вы дробями в повседневной жизни? Примеры.

VИ. Домашнее задание

§ 22. I и II уровень № 1018, III уровень № 1021, VИ уровень № 1023 (б), № 1025.

Приложения

Историческая справка

Вы уже знаете, что натуральные числа возникли в результате практической деятельности людей, которым надо было считать животных, предметы, измерять длины, площади, объемы. Но результат измерения не всегда можно обозначить натуральним числом, потому что в результате измерений чаще всего достаем части принятой единицы.

Так на основе потребностей практики возникло понятие дроби - числа, состоящий из нескольких одинаковых частей единицы.

В Египте с дробями оперировали еще 4000 лет поэтому. Об этом свидетельствуют древние документы, которые сохранились с тех времен. Однако общего способа для обозначения всех дробей, как где принято теперь, когда числитель записывают сверху, знаменник снизу, а между ними ставят черту, у египтян не было. При выполнении вычислений древние египтяне застосовували только так называемые единичные дроби - дроби ссельником 1 (дробь ). Такие дроби египтяне изображали, ставя точку над знаменателем. Все остальные дроби они возводили до единичных. Например, дробь подавали ввиде суммы единичных дробей и . Для возведения дробей к единичных были составлены специальные таблицы.

Вавилоняне пользовались лишь шістдесятковими дробами, то есть дробями, знаменатели которых равны 60 или произведения чисел, каждое из которых равнялось 60, наприклад:

60 ∙ 60 = 3600; 60 ∙ 60 ∙ 60 = 216 000 и т. д. Это отповедало принятой там шістдесятковій нумерации - применения шістдесяткових дробей значительно упрощало розв'ятельства практических задач.

Вавилоняне много сделали в области астрономии. Поэтому и не удивительно, что шістдесятковими дробями пользовались в астрономических вычислениях вплоть до XVII в. ученые других народов и называли эти дроби астрономическими.

В отличие от этих дробей, дроби с любым знаменником назвали обычными.

В древней Греции обыкновенные дроби были известны. Более 2,5 тысячи лет назад греки умели выполнять арифметичні действия с обыкновенными дробями. Они пользовались и единичными дробями, и дробями общего вида.

В древней Руси дроби называли долями», а позжедом «ломаными числами». Отдельные дроби имели специальные названия.

Например, - треть, - півтреть, - пятина, - десятина т.д./span>

Запись дробей с помощью черточки стал загальноприйнятем с XVI ст.

Когда действия с обыкновенными дробями наносили людям надобычных затруднений. Эти трудности в Вавилоне объясняли «вмешательством злых духов».

Английский монах Беда (VII в.), который был ученым человеком своего времени, писал: «В мире есть много вещей, но нет ничего труднее, чем четыре действия арифметики».

Тогда же, видимо, и возникло немецкая пословица «попасть в дроби», что означало оказаться в затруднительном положении. А причина, конечно, заключалась в том, что не было установлены правил выполнения действий с дробями, не было создано соответствующей теории.

Наряду с этим в VII в. известный армянский ученый Анания Ширакаци (Ширака) умел добавлять к восьми дробей с разными знаменателями.

О математике Анания говорил: И очень полюбив искусство численное, помыслил я, что без числа никакое рассуждение философское не состоит. Всей мудрости матерью его считая”. Особый интерес представляют учебник и задачник по арифметике, который составил Анания. В нем приводится решение задач, содержащих сложение дробей, среди знаменателей которых есть числа: 7, 8, 9, 13, 14, 16, 20.