УРОК 66
Тема. Представление о
обыкновенные дроби
Цель: закрепить
знания учащихся по чтению, записи дробей и решения задач на
нахождение дроби от числа, а также дополнить эти знания алгоритмом решения
задачи на нахождение числа по его дроби.
Тип урока:
усвоение знаний, умений, навыков.
Ход урока
И. Проверка
домашнего задания
Письменную часть
домашнего задания учитель проверяет только у слабых учащихся, собрав их
тетради перед уроком. На уроке проверяются усвоение теоретических знаний и
способов действий. Учащимся предлагается выполнить устные упражнения.
1.
Прочитайте
дроби, назовите в каждом из них числитель и знаменатель:
1) 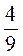 ; 2)
; 2) 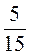 ; 3)
; 3) 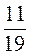 ; 4)
; 4) 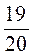 ; 5)
; 5) 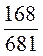 .
.
2.
Наведите
пример дроби:
1) знаменатель которого
на 5 больше числитель;
2) числитель которого
втрое меньше знаменателя.
3. Петя покрасил забор за 4 ч. Которую
часть забора он покрасил за 3 ч.?
4. Сад прямоугольной формы имеет длину 40 м,
ширину 30 м. Вишни занимают 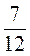 сада. Сколько
аров засажено вишнями?
сада. Сколько
аров засажено вишнями?
5. Сравните:
1) 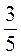 дм и 5 см;
дм и 5 см;
2) 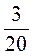 час. и 18 мин.;
час. и 18 мин.;
3) 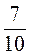 т и 695 кг;
т и 695 кг;
4) 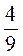 прямого угла и 49°.
прямого угла и 49°.
II. Актуализация опорных знаний
Осуществляется под
время выполнения учащимися устных упражнений, если учитель требует от них делать
объяснение.
III. Дополнение знаний
1. Известно, что одной банки краски хватает, чтобы
покрасить 100 м2 пола. Какая часть краски останется после того,
как покрасят пол в кабинете шириной 5 м и длиной 8 м?
2. Покрасив 10 м2 пола,
выяснили, что потрачено 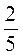 банки краски.
Хватит ли этого, чтобы покрасить пол, если комната имеет
размеры 5 м х 8 м?
банки краски.
Хватит ли этого, чтобы покрасить пол, если комната имеет
размеры 5 м х 8 м?
[Решения. 1) 10
: 2 = 5 (м2) - на сколько хватит 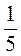 банки;
банки;
5 · 5 = 25 (м2)
- на сколько хватит всей банки;
5 · 8 = 40 (м2)
- площадь пола;
25 40, следовательно,
не хватит.]
После решения
задач учитель отмечает, что понятие дробей помогает решать как
задачи на нахождение какой-то части (дроби) от данного числа, так и обратные
задачи (по дробью найти число), разбираются задачи № 2, 3, решены в п.
22 учебника.
IV. Закрепления знаний.
Решение упражнений
1. Простейшие задачи на нахождение числа по
его дробью № 666, 668.
2. № 675, 679 - арифметические задачи на
нахождение дроби от числа.
3. № 685 - задачи на движение с применением
алгоритма нахождения числа по его дроби.
4. № 687 - комбинированная задача (найти дробь от
числа и затем число по его дроби).
Дополнительные (логические)
упражнения
1.
Которое с
представленных чисел надо выбрать? (рис. 98)

2.
Найти
пропущенное число (рис. 99)
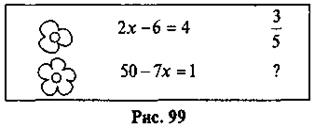
V. Домашнее задание
п. 222, № 667; 669;
676; 678; 686; на повторение № 691 (2).