УРОК 63

Тема. Деление с остачею. Площадь прямоугольника. Прямоугольный параллелепипед и его объем

Цель: подготовить учащихся к тематической аттестации.

Тип урока: обобщение и систематизация знаний.

Оборудование: таблицы «Деление с остачею», «Площадь прямоугольника», «Объем прямоугольного параллелепипеда».

Ход урока

I. Проверка домашнего задания (Собрать тетради)

II. Актуализация опорных знаний

Устные упражнения

1. Найдите часть и остаток от деления:

1) 49 на 10; 2) 49 на 9; 3) 49 на 7; 4) 49 на 48.

2. Вычислите значение выражения: 1) 2³; 2) 3²; 3)1¹²⁵; 4) (5 - 5)¹⁰⁰.

3. Найдите периметр квадрата, площадь которого равна площади прямоугольника со сторонами 4 см и 9 см.

4. Объем прямоугольного параллелепипеда равен 240 см³. Которая с преемник троек чисел может задавать замеры этого параллелепипеда?

1) 4 см, 6 см, 12 см;

2) 5 см, 6 см, 8 см;

3) 3 см, 5 см, 10 см.

5. Почему равна сумма длин всех ребер этого параллелепипеда? Хватит ли 200 см² цветной бумаги, чтобы обклеить модель этого параллелепипеда со всех сторон?

II. Обобщение и систематизация знаний

После решения устных упражнений учитель еще раз повторяет с учащимися основной теоретический материал раздела (удобнее будет сделать это с помощью таблиц «Деление с остачею», «Площадь прямоугольника», «Объем прямоугольного параллелепипеда»). Задает вопрос:

1. Как найти делимое, если известен делитель, неполное доля и остаток?

2. Некоторое число разделили на 7, получив в части 3 и в остатка 8. Может ли такое быть? Почему?

3. Как измеряется площадь фигуры? Какая единица (измерения) площади в 10 раз больше 1 мм² (1 см², 1 дм², 1м²)?

4. Какие замеры нужно сделать, чтобы вычислить: 1) площадь прямоугольника, изготовленного из бумаги; 2) площадь квадратного участка земли? А как вычислить их периметры?

5. Как измерить объем геометрического тела? Которую единицу объема получим, если 1 мм³ увеличить в 1 000 000 раз?

6. Дано деревянную модель прямоугольного параллелепипеда. Какие замеры нужно сделать, чтобы вычислить: 1) его объем; 2) площадь поверхности; 3) длину всех его ребер? Изменится ли решение задачи, если вместо параллелепипеда взять куб?

Повторив теоретический материал, учащиеся могут переходить к решению письменных упражнений. (Желательно обратиться к рабочих тетрадей - тематическое оценивание № 5.)

@ Учитель может организовать работу учащихся на уроке различными способами: самостоятельная с последующей проверкой и объяснениями непонятных моментов; работа учащихся на местах с комментарием кого-нибудь из учеников с места; фронтальное решение упражнений у доски. В любом случае надо следить за тем, чтобы ученики как можно чаще повторяли соответствующий теоретический материал (в случае объяснений, комментариев и т.п.).

Дополнительные задания

Задача 1. Как вычислить количество коробок со спичками в ящике, не распаковывая его, если есть одна из таких коробок?

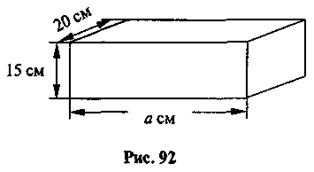
Задание 2. Коробку, изображенную на рис. 92, необходимо оклеить бумагой так, чтобы левая и правая боковые грани остались необклеєними. Выражение задает площадь необходимого для этого листа бумаги (в см²)?

1) (15 + 20) · 2а;

2) (15 + 20) · a;

3) (а + 15) · 20;

4) (а + 20) · 15.

III. Домашнее задание

Повторить пп. 18-21, №№ 536 (4-6); 539 (найти 5); 590; 619; 620; 637.