УРОК № 63

Тема. Неравенства с одной переменной

Тестовые задания

1. Даны неравенства:

1) -2х2 + х + 6 0;

2) 2х2 + х + 7 ≥ 0;

3) х2 > 0;

4) -3х2 - х - 6 0.

2. Какая из данных неравенств выполняется при любых значениях x?
а) все; б) 2; 3; в) 3; 4; г) 2; 4.

3. Решите неравенство: 15х2 + 8х + 1 ≥ 0.
а) ;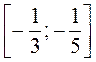

б) ;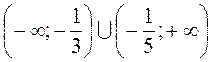

в) ;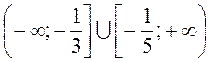

г) .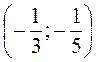

4. Решите неравенство 3х2 - 12 ≤ 0.

а) (-∞; 2]; б) (-∞; 4]; в) [-2; 2]; г) (-∞; -2]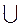[2; +∞).

5. Найдите область определения функции .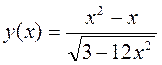

а) (-∞; 4)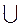(4; +∞);

б) ;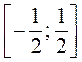

в) ;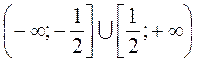

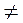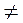г) х 0, х 1.

6. Решите двойное неравенство: -3 ≤ 2x2 - x ≤ 1.
а) (-∞; +∞); б) [-0,5; 1]; в) [-1; 0,5]; г) другой ответ.

7. Какая из данных неравенств равносильна неравенству (3 - х)2 > 0 ?

а) 3 - х 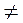0; б) 3 - х 0; в) 3 - х > 0; г) 3 - х = 0.

Письменные упражнения

1. При каких значениях переменной х значение выражения 3х(х - 4) - (3x + 2)(3х - 2) не менее от -4?

2. При каких значениях т уравнение х2 +тх + 2 = 0 имеет два различных действительных корня?

3. Найдите область определения функции y = + .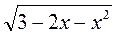

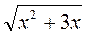4. Найдите все значения переменной, при которых значение выражения (х - 2)2(х2 - 3х + 2) является неотрицательным числом.

5. Решите неравенство (х2 + 4)(х2 - 4х + 3) ≥ 0.

6. Найдите, при каких значениях т неравенство mx2 + 5mx + 4m + 3 0 не имеет решений.