2-й семестр

МЕХАНИКА

4. Механические колебания и волны

Урок 2/61

Тема. Гармонические колебания

Цель урока: ознакомить учащихся с понятием гармонических колебаний

Тип урока: изучение нового материала

План урока

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

1. Сравнение колебательного движения и равномерного движения по окружности

Колебательное движение и равномерное движение по кругу очень похожи: оба эти периодические движения, они характеризуются схожими физическими величинами. Можно предположить, что и уравнение координаты материальной точки, движущейся по окружности, и уравнение координаты колеблющейся материальной точки могут иметь одинаковый вид.

Сравним два движения: колебания легкого подвижного тележки, прикрепленного к вертикальной стене с помощью мягкой пружины, и движение по кругу шарики, закрепленной на диске, который вращается.

Выведем тележка из положения равновесия. Он начнет совершать колебательное движение с частотой ν = N/t.

Соберем установку, показанную на рисунке. Обертатимемо диск с частотой, равной частоте колебаний тележки. Во время вращения диска тень шарика совершает колебательное движение. Если растянуть пружину на расстояние, равное радиусу вращения шарика (А = r), и отпустить ее в тот момент, когда тень от шарика на диске совпадет с тенью от шарика на коляске, то увидим, что колебание тени от шарика и колебания тени от коляски абсолютно одинаковые.

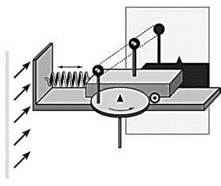
2. Гармонические колебания

Изучая движение материальной точки по окружности, мы отмечали, что координата материальной точки менялась по закону синуса или косинуса. Обратим внимание на расположенный ниже рисунок.

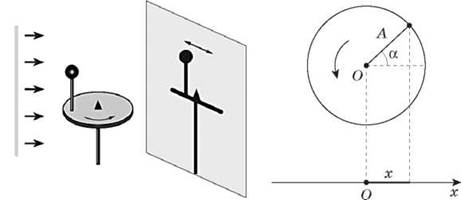
Если обозначить радиус окружности, которую описывает шарик, через А, а начало координат совместить с центром круга, то проекция радиус-вектора шарика на ось Ох будет равна х = Acosφ, где φ - угол, на который повернулась шарик.

В случае равномерного движения по окружности φ = ωt, где ω = 2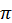/T - угловая скорость вращения шарика. Следовательно, уравнения движения тени шарика вдоль оси Ох имеет вид:

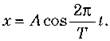
Поскольку тень от шарика и тень от тележки совершают абсолютно одинаковые движения, то уравнение колебаний точки на коляске будет одинаковым:

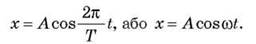
В этом уравнении х - координата точки в любой момент времени t; А - амплитуда колебаний; Т - период колебаний; ω = 2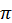/T - циклическая частота. Начало координат совпадает с точкой, в которой тележка находится в состоянии равновесия.

Ø Колебания, когда координата тела изменяется с течением времени по закону косинуса (или синуса), называются гармоническими.

Тележку, закрепленный на пружине, совершает гармонические колебания.

3. Фаза колебаний

Запишем еще раз уравнение гармонических колебаний:

Обозначим величину, которая записана под знаком косинуса, φ.

Ø Фаза колебаний - это величина, которая записывается под знаком ко синуса или синуса в уравнении гармонических колебаний:

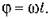
Фаза колебаний определяет при заданной амплитуде состояние колебательной системы в любой момент времени. Колебания с одинаковыми амплитудами и частотами могут отличаться друг от друга фазами.

Если, изучая колебательное движение, включают секундомер не в тот момент, когда амплитуда колебаний была максимальной, а через некоторый промежуток времени, то уравнение колебаний будет иметь вид:

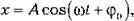
где φ0 - начальная фаза, то есть фаза колебаний в момент времени t0 = 0.

Если начало отсчета времени совпадает с моментом пребывания тела в положении равновесия, то в этот момент координата тела равна нулю, поэтому в этом случае уравнение колебаний имеет вид:

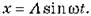
Собственно говоря, колебания отличаются только начальными фазами. По уравнениям колебаний легко определить все кинематические характеристики колебательного движения.

4. Графики гармонических колебаний

График зависимости координаты колеблющегося тела от времени называют графиком колебаний.

На рисунках показаны графики гармонических колебаний координаты тела изменяется по закону х = Asinωt (рис. а) и по закону x = Acosωt (рис. б).

По графикам колебаний легко определить все кинематические характеристики колебательного движения и записать уравнение колебаний.

Вопрос к ученикам во время изложения нового материала

1. Что общего между колебательным движением и равномерным движением по окружности?

2. Приведите примеры гармонических колебаний.

3. Какая кривая является графиком свободных колебаний при отсутствии трения?

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

1). Тренируемся решать задачи

1. Колебания груза на пружине описывается уравнением х = 0,1sin0,57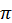t. Вычислите амплитуду, период, циклическую частоту и частоту колебаний.

2. Амплитуда колебания 2 см, смещение - 1 см. Сколько времени прошло от момента начала колебаний?

Решение

Если бы движение было равномерным, то ответ был бы: t = 1/8T. Но движение груза в этой задаче неравномерный.

Уравнение движения имеет вид: 1 = 2cosωt, откуда: cosωt = 1/2. Следовательно, ωt = 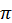/3, откуда: 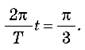Таким образом, t = T/6.

3. На рисунке приведен график гармонического колебания. Вычислите амплитуду, частоту и период колебания. Запишите формулу зависимости х(t).

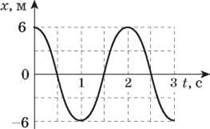
2). Контрольные вопросы

1. Какая кривая является графиком свободных колебаний груза на пружине и отделов камертона?

2. Каким уравнением вы будете пользоваться, если в момент начала наблюдений тело находилось в положении равновесия? Тело было максимально отклонен от положения равновесия?

3. Какую часть периода составлял время движения маятника, если он отклонился от положения равновесия до крайнего положения? дошел до крайнего положения и вернулся в положение равновесия?

Что мы узнали на уроке

• Колебания, когда координата тела изменяется с течением времени по закону косинуса (или синуса), называются гармоническими:

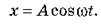
• Фаза колебаний - это величина, которая записывается под знаком косинуса или синуса в уравнении гармонических колебаний:

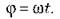
Домашнее задание

1. П.: § 40.

2. 36.: № 20.4; 20.17; 20.18; 20.24, 20.25.