Урок № 62
Тема. Решение задач
Цель: сформировать представление учащихся о схеме решения задач на совместную работу составление дробно-рационального уравнения; сформировать умение применять составленную схему решения текстовых задач на совместную работу.
Тип урока: применение умений и навыков.
Наглядность и оборудование: опорный конспект «Решение задач составлением уравнений».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
С целью эффективной и быстрой проверки правильности выполнения упражнений домашней работы предлагаем учащимся выполнить работу по заполнению таблицы, аналогичной таблице предыдущего урока (см. урок 61). После выполнения работы - обязательная коррекционная работа.
III. Формулировка цели и задач урока
Для создания положительной мотивации учебной деятельности учащихся предлагается решить задачу на совместную работу, что приведет к составление линейного уравнения (известно); после этого предлагаем похожую задачу, решение которой приведет к составлению ДРР. Осознание учащимися противоречие между известным и неизвестным означает существование проблемы. Решение этой проблемы - овладение способами действий для решения задач составлением уравнений на совместную работу - это главная цель урока.
IV. Актуализация опорных знаний и умений
@ С целью успешного восприятия учащимися учебного материала урока следует активизировать знания и умения учащихся: выполнения тождественных преобразований рациональных выражений; применение различных способов решения квадратных уравнений различных видов; решения ДРР; составление выражений с переменными, которые соответствуют условию задачи.
Выполнение устных упражнений
1. При каких значениях х имеет смысл выражение: а) 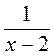 ; б)
; б) 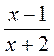 ; в)
; в) 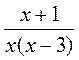 ; г)
; г) 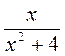 ; д)
; д) 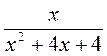 ?
?
2. Решите уравнение: а) 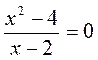 ; б)
; б) 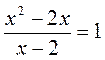 ; в)
; в) 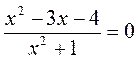 .
.
3. Комбайнер может убрать урожай с участка за а дней. Какую часть урожая он может собрать за 1 день? Решить задачу при а = 7; 11; 3,5.
V. Формирование умений
Выполнение письменных упражнений
Для реализации дидактической цели урока следует решить задачи следующего содержания:
1. Решение задач на совместную работу.
1) Два экскаватора, работая вместе, вырыли канаву за 3 ч 45 мин. Первый экскаватор, работая один, может вырыть канаву на 4 ч быстрее, чем второй. За какое время может вырыть канаву каждый экскаватор, работая отдельно?
2) Первая бригада может проложить дорогу на 3 дня быстрее, чем вторая. Если первая бригада проработает 6 дней, а потом вторая - 4 дня, то они проложат всю дорогу. За сколько дней может проложить дорогу первая бригада?
3) Один штукатур может выполнить задание на 5 часов быстрее, чем второй. Вместе они выполнят это задание за 6 часов. За сколько часов каждый из них выполнит задание?
2. Решение задач на движение.
1) Пароход проплыл 18 км по течению реки и 16 км против течения. Па путь по течению реки он затратил на 15 мин меньше, чем на путь против течения. Найдите скорость течения реки, если скорость парохода в стоячей воде 20 км/ч.
2) Два самолета вылетели одновременно с одного аэродрома на другой, расстояние между которыми 1800 км. Скорость одного самолета на 100 км/ч меньше скорости другого, поэтому он прибыл в назначенный пункт на 36 минут позже. Найдите скорость каждого самолета.
3. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний.
1) Два экскаваторы различной мощности могут вырыть котлован за 4 дня. Треть котлована первый экскаватор может вырыть на 2 дня быстрее, чем второй. За сколько дней может вырыть котлован каждый экскаватор, работая отдельно?
2) Два бавовнозбиральних комбайны вместе могут собрать хлопок с поля на 9 дней быстрее, чем первый комбайн, и на 4 дня быстрее, чем второй. За сколько дней каждый комбайн может собрать всю хлопок?
3) Для наполнения бассейна через первую трубу потребуется на 9 часов больше времени, чем во время наполнения через первую и вторую трубы, и на 7 часов меньше, чем через одну вторую трубу. За сколько часов наполнится бассейн через обе трубы?
4. На повторение: решение уравнений, сводящихся к квадратным.
1) Решите уравнение:
а) (х + 4)(х - 1) - 5х = 2х2 - 4;
б) (х - 3)2 - (3х - 5)2 = 0.
2) Решите уравнение:
а) (х2 - х)2 + х2 - х = 6;
б) (3х2 + 2х)2 - 4(3х2 + 2х) - 5 = 0;
в) (х2 + х + 1)(х2 + х + 2) = 12;
г) (х2 - 4х + 1)(х2 - 4х - 3) = 12.
3) Решите уравнение х + 3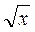 - 4 = 0.
- 4 = 0.
@ Традиционно задачи на совместную работу являются наиболее сложными для понимания учащимися. Преодоление этих трудностей может осуществляться двумя способами. Или решать эти задачи как задачи на движение, где часть работы, выполненная за единицу времени, рассматривается как аналог скорости, а выполнена за время t часть работы рассматривается как аналог расстояния. Второй путь преодоления трудностей - изучение специфической схемы действий в решении задач на совместную работу, записанную в виде таблицы:
|
1-й рабочий |
2-й рабочий |
Время на выполнение всей работы каждым |
|
|
Часть работы, выполненная за один час |
|
|
Время, использованное на выполнение совместной работы |
|
|
Часть работы, выполненная за это время |
|
|
VI. Итоги урока
Самостоятельная работа 15
Вариант 1 |
Вариант 2 |
1. Найдите стороны прямоугольника, периметр которого равен: |
32 см, |
40 см, |
а площадь равна: |
55 см2 |
51 см2 |
2. Моторная лодка прошла 60 км по течению реки и 36 км по озеру, затратив на весь путь 5 ч. Найдите собственную скорость лодки, если скорость течения 5 км/ч |
2. Расстояние между двумя пристанями 112 км. Двигаясь по течению, катер преодолел это расстояние на 1 час быстрее, чем во время обратного пути. Найдите собственную скорость катера, если скорость течения 1 км/ч |
VII. Домашнее задание
1. Повторить изученные на протяжении последних уроков схемы действий.
2. Решить задачи на применение изученных схем действий.
3. Повторить темы «Квадратный трехчлен», «Решение уравнений, сводящихся к квадратным».
(Как вариант домашнего задания - домашняя самостоятельная работа.)
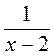 ; б)
; б) 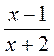 ; в)
; в) 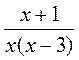 ; г)
; г) 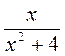 ; д)
; д) 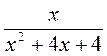 ?
?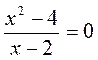 ; б)
; б) 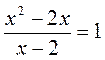 ; в)
; в) 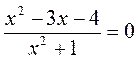 .
.