УРОК 61
Тема. Решение логарифмических неравенств
Цель урока. Формирование умений учащихся решать логарифмические неравенства
И. Проверка домашнего задания
Проверить наличие выполненных домашних заданий и ответить на вопросы, возникшие у учащихся при выполнении этих заданий.
II. Восприятие и осознание решения логарифмических неравенств (которые решаются введением новой переменной)
Пример 1. Решите неравенство log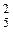 x - log5 x > 2.
x - log5 x > 2.
Решение
Пусть log5х = у, тогда получим неравенство у2 - у - 2 > 0.
Решим полученное неравенство методом интервалов (рис. 171): y 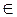 (-
(- ; -1)
; -1)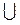 (2; +
(2; + ).
).
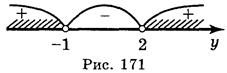
Учитывая замену получим:
1) log5 x -1; log5 x log5  ;
; 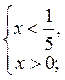 х
х 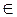
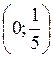 ;
;
2) log5 x > 2; log5 x > log525; 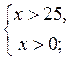 x
x 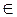 (25; +
(25; + ). Следовательно,
). Следовательно, 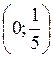
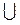 (25; +
(25; + ) - решение данного неравенства.
) - решение данного неравенства.
Ответ: 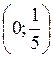
 (25; +
(25; + ).
).
Пример 2. Решите неравенство 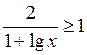 .
.
Решение
Пусть lg x = у, тогда получим неравенство
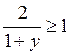 ; в ≠ 1;
; в ≠ 1; 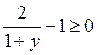 ;
; 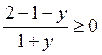 ;
; 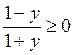 .
.
Решим полученное неравенство методом интервалов (рис. 172): в 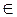 (-1; 1].
(-1; 1].
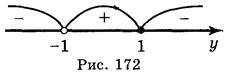
Учитывая замену, получим -1 lg x 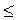 1.
1.
Тогда 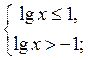
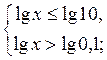
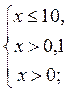 следовательно, х
следовательно, х 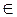 (0,1; 10] (рис. 173).
(0,1; 10] (рис. 173).
Ответ: (0,1; 10].
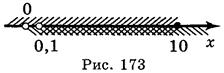
III. Формирование умений решать логарифмические неравенства
Выполнение упражнений№ 59 (10), 60 (15).
IV. Восприятие и осознание решения логарифмических (комбинированных) неравенств методом интервалов
Пример 1. Решите неравенство (3х - 6)log0,5 x > 0.
Решение
Пусть в = (3х - 6) log0,5 x, у > 0.
Область определения функции: х > 0.
Найдем нули функции: (3х - 6) · log0,5 x = 0;
3х - 6 = 0, log0,5 х = 0;
х = 2, х = 1.
Разобьем область определения функции на промежутки точками 2 и 1 и найдем знаки функции на образовавшихся промежутках (рис. 174). Следовательно, х 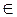 (1; 2).
(1; 2).
Ответ: (1; 2).
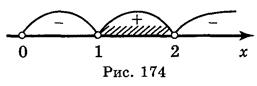
Пример 2. Решите неравенство log x-3(х - 1) 2.
Решение
Пусть у = log x-3(х - 1) - 2 и в 0. Область определения функции находим из системы: 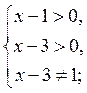
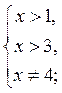 х
х 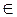 (3; 4)
(3; 4) 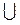 (4; +
(4; + ).
).
Найдем нули функции: log x-3(х - 1) = 2; х - 1 = (х - 3)2; х - 1 = х2 - 6х + 9; х2 - 7х + 10 = 0; х = 5, х = 2. х = 2 - не входит в область определения функции. Проверкой убеждаемся, что х = 5 - нуль функции.
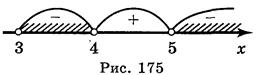
Разобьем область определения функции на промежутки точкой 5 и найдем знаки функции на образовавшихся промежутках (рис. 175).
Следовательно, х 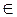 (3; 4)
(3; 4) 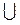 (5; +
(5; + ).
).
Ответ: (3; 4) 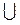 (5; +
(5; + ).
).
V. Формирование умений решать логарифмические неравенства
Выполнение упражнений№ 59 (8), 60 (12).
VI. Восприятие и осознание графического способа решения логарифмических неравенств
Пример. Решите неравенство log3 x 4 - х графически.
Решение
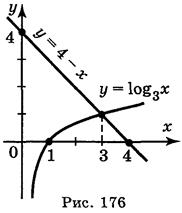
Построим графики функций у = log3 x и у = 4 - х в одной системе координат. Графики пересекаются в точке А с абсциссой х = 3 (рис. 176).
Из рисунка видно, что множество решений неравенства log3 x 4 - х является промежуток (0; 3].
Ответ: (0; 3].
VII. Подведение итогов урока
VIII. Домашнее задание
Подготовиться к тематической контрольной работы. Упражнения№ 59 (7; 9), 60 (11).